Can Juliet manage without Romeo? How much she should spend, save, and invest to achieve that?

Meet Juliet

Juliet just turned 20 and is ready to start her adult life. She’s landed a stable, well-paid job and her new journey begins. This time, life unfolds without Romeo. Think she can’t handle it? You might be surprised.

Juliet feels anxious about her future. Each month she have to choose how to balance spending, saving, and investing for what’s ahead. She’s keen to avoid poor decisions. Juliet seeks clear, rational advice tailored to her needs—not the generic advice that’s all over the internet. She aims to make informed, personalized financial choices that align with her present knowledge and future plans. She needs a clear set of recommendations to know how much to save and how to invest ¹.

Let’s follow Juliet’s example to craft a straightforward financial report for a single-person household. We will be using our new R4GoodPersonalFinances R package that implements (with our modifications) the theoretical model invented and described in Lifetime Financial Advice: A Personalized Optimal Multilevel Approach by Thomas M. Idzorek and Paul D. Kaplan (Idzorek and Kaplan 2024).

Juliet’s assumptions and expectations

We aim to explore scenarios that an individual might encounter, based on realistic assumptions about market returns and living expenses in a big Polish city. These scenarios reflect a consistent, median-level income. We focus on income and spending estimates for Poland, using Polish złoty (PLN). However, you can adapt these scenarios to any currency or country-specific factors.

Code

monthly_income                   <- 4995
monthly_social_security_benefits <- 1710
monthly_cost_of_living           <- 3500

Juliet, a 20-year-old young woman that leaves in a big city in Poland, chooses to stay single. She imagines this will be her lifelong path.

Juliet has just got a job, so she expects a steady income of 4’995 PLN net salary per month (real / inflation-adjusted). When she retires (at the age of 60 or later) she will receive a pension from Polish social security (emerytura ZUS) of 1’710 PLN per month (in today’s money and inflation-adjusted).

Juliet plans to spend 3’500 PLN each month on her basic needs. This covers her essential, non-discretionary expenses. Beyond that, she would like to allocate some funds for discretionary spending – the things that bring her joy.

Juliet holds modest savings of 1’500 PLN, already invested in two assets: a global stock ETF and Polish inflation-protected bonds, known as EDO.

Juliet aims to apply a lifecycle model to pinpoint her optimal discretionary spending and asset allocation. She also wants to explore how her discretionary spending might shift if she retires at various ages.

Setting up the technical essentials for the report

Loading the package

Code

library(R4GoodPersonalFinances)

Welcome to R4GoodPersonalFinances version 1.1.0!

Cite the package: citation('R4GoodPersonalFinances')

Package documentation: https://r4goodacademy.github.io/R4GoodPersonalFinances/

To learn more, visit: https://www.r4good.academy/

... and Make Optimal Financial Decisions!

Setting the date of the report

We start with setting one common current_date for all analyses in the report. Let’s assume that the current date is 2025-01-01. We could set the current_date parameter in each function call, but we can also set it as a global option for the entire R session - like in our example.

If we didn’t set the current_date parameter, it would be set to the current computer date by default. As a result, the report cold not be the same if rendered for different dates. So for reproducibility, we set the current_date to this arbitrary date 2025-01-01 for the whole R session.

Code

options("R4GPF.current_date" = "2025-01-01")

Creating Juliet’s household

Defining the household member

First, we need to create an object of HouseholdMember class that represents Juliet.

Code

juliet <- HouseholdMember$new(
  name       = "Juliet",  
  birth_date = "2005-01-01"
)  
juliet

── "Juliet"

ℹ Birth date: 2005-01-01

ℹ Current age: 20 years

ℹ Max age: 100 years

ℹ Max lifespan: 80 years

ℹ Gompertz mode: NA

ℹ Gompertz dispersion: NA

ℹ Life expectancy: NA years

Juliet came into this world on January 1, 2005—exactly 20 years before the report’s date, January 1, 2025. By default, her maximum age is 100 years. So, her remaining lifespan is 80 years, calculated as maximum age minus current age (100 - 20 = 80).

We haven’t determined mode and dispersion for the Gompertz model yet, so life expectancy remains unclear. Let’s address that now.

Setting Gompertz parameters for Juliet

Let’s find Julia’s Gompertz parameters: mode and dispersion. We’ll calculate these using data from a typical 20-year-old Polish woman and then apply them to Julia.

Tip

Discover why Gompertz parameters matter and how to model them here: How to model our probability of survival?

Code

gompertz_parameters <- 
  get_default_gompertz_parameters(
    age     = juliet$calc_age(), 
    country = "Poland", 
    sex     = "female"
  )

juliet$mode       <- gompertz_parameters$mode
juliet$dispersion <- gompertz_parameters$dispersion
juliet$max_age    <- gompertz_parameters$max_age
juliet

── "Juliet"

ℹ Birth date: 2005-01-01

ℹ Current age: 20 years

ℹ Max age: 97.8 years

ℹ Max lifespan: 77.8 years

ℹ Gompertz mode: 89

ℹ Gompertz dispersion: 10.08

ℹ Life expectancy: 83.3 years

We estimate Juliet could live up to 97.8 years, with an expected lifespan of about 83.3 years.

Defining Juliet’s household

Let’s start a household with Juliet. Juliet is the lone member, but she is welcome to add others as needed in the future.

Code

household <- Household$new()
household$add_member(juliet)  
household

── Household ───────────────────────────────────────────────────────────────────

ℹ Current date: 2025-01-01

ℹ Household lifespan: 78 years

ℹ Consumption impatience preference: 0.04

ℹ Smooth consumption preference: 1

ℹ Risk tolerance: 0.5

── Household members ──

── "Juliet"

ℹ Birth date: 2005-01-01

ℹ Current age: 20 years

ℹ Max age: 97.8 years

ℹ Max lifespan: 77.8 years

ℹ Gompertz mode: 89

ℹ Gompertz dispersion: 10.08

ℹ Life expectancy: 83.3 years

You can see that we successfully added Juliet to her household.

Juliet’s household comes with preset preferences. Key ones include:

Consumption impatience.
Smooth consumption.
Risk tolerance.

Future posts will explore these preferences in detail and offer tips on customization. For now, let’s assume that default values of those preferences are sensible and will work for Juliet well enough.

Juliet’s lifespan matches that of her household since she’s its sole member. You can visualize the lifespans of household members by plotting their age-of-death probability distributions and life expectancy.

Code

household |> plot_life_expectancy()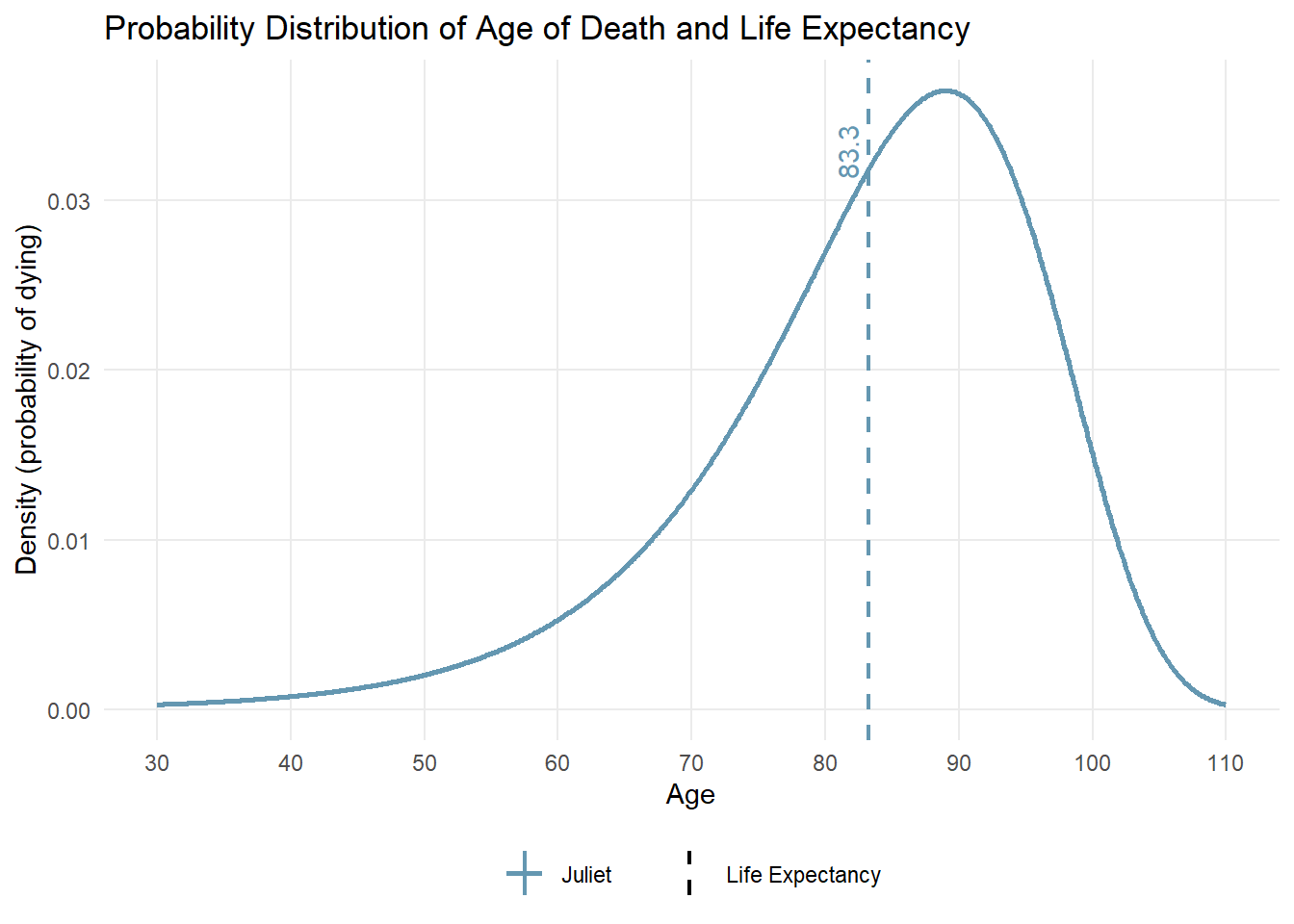

On the plot, Juliet sees her life expectancy is 83.3 years. She knows this is just an estimate; her actual lifespan could be shorter or longer. The life-cycle model takes into account all probabilities tied to different lifespans.

She may consider in the future adjusting the Gompertz parameters to match her life expectancy expectations. For now, she’s content with the defaults.

Defining income and spending expectations

We need to define both income and spending in “real” terms to account for inflation over time. For instance, setting a real income of 1 000 PLN implies it maintains its purchasing power and increases with inflation. This way, years later, you can still buy what 1 000 PLN can buy today. This is a reasonable, though optimistic, expectation for salary and more realistic for inflation-adjusted social security pensions.

We need to set expected annual income and expenses. If you have a monthly amount, multiply it by 12 for the yearly total.

We’ll demonstrate next how to define cash flow streams linked to events affecting a household member. In this case, we’ll focus on income changes tied to a retirement event and Juliet’s age.

Setting the `retirement` event

Code

retirement_start_age <- 60

As Juliet expects to retire at the age of 60 years, we set the retirement event to start at this age. We also assume that Juliet will be retired till the end of her life.

Code

juliet$set_event("retirement", start_age = retirement_start_age)

Setting expected disposable income streams

Juliet expects that in her lifetime she will be receiving two income streams: salary income and social security pension income.

The income needs to be defined as net disposable income - the after-tax income that Juliet can spend on stuff she needs and wants (non-discretionary and discretionary spending).

Salary income

Juliet is moderately optimistic about her future income. She expects to make 4’995 PLN net salary per month (after taxes). This is coincidentally the median net salary in Poland in November 2024².

Pension income

Juliet also expects to receive a pension from Polish social security (emerytura ZUS) of 1’710 PLN per month. This is coincidentally the net minimum social security pension in Poland in 2025³.

Juliet is rather conservative in this believe, as her social security benefits will be probably higher than the minimum, especially if she decides to work longer, and claims the benefits at a later age (more about this later).

Setting rules for income streams

Alright, we have what we need to set up rules triggering different income streams for Juliet, based on her age and the retirement event.

We’re defining a salary income stream, which provides funds while Juliet isn’t retired. The social security benefits stream activates when Juliet retires at 60 (Poland’s minimum age for women to claim these benefits) or later.

Code

household$expected_income <- 
  list(
    "salary income" = c(
      glue::glue(
        "is_not_on('Juliet', 'retirement') ~ {monthly_income * 12}"
        )
    ),
    "social security benefits" = c(glue::glue(
      "is_on('Juliet', 'retirement') & age('Juliet') >= 60 ~ ",
      "{monthly_social_security_benefits * 12}"
    ))
  )
household$expected_income

$`salary income`
[1] "is_not_on('Juliet', 'retirement') ~ 59940"

$`social security benefits`
[1] "is_on('Juliet', 'retirement') & age('Juliet') >= 60 ~ 20520"

Setting expected non-discretionary spending

Juliet must identify her essential expenses. Non-discretionary spending covers basic needs such as food, clothing, housing, transport, and medical care. She estimates these costs at 3,500 PLN monthly for living alone in a big city in Poland ⁴.

Let’s keep it simple. Non-discretionary spending stays the same, even after retirement. But discretionary spending? That changes. Juliet wants to know how much is optimal for her.

Code

household$expected_spending <- 
  list(
    "total non-discretionary spending" = glue::glue("TRUE ~ {monthly_cost_of_living * 12}")
  )
household$expected_spending

$`total non-discretionary spending`
TRUE ~ 42000

Important

Non-discretionary spending can vary even within the same category. Take transport, for instance. City bus fares might be essential, yet driving a personal car could be viewed as optional. The distinction often hinges on individual circumstances and assessments.

Creating Juliet’s portfolio

Let’s set up Juliet’s portfolio with a simple template, mostly keeping the defaults. Juliet invests her savings in two assets: a global stock index fund or ETF, and Polish inflation-protected bonds (EDO).

She already has some savings in Polish inflation-protected bonds: 1’000 PLN in a taxable account and 500 PLN in a tax-advantaged account such as IKE.

Juliet views her human capital (discounted future income) and liabilities (discounted future non-discretionary spending) as bond-like—steady and rather uncorrelated to the stock market. This perspective makes sense for many but should be tailored to fit each person’s situation⁵.

We’ll build Juliet’s portfolio, incorporating relevant defaults for Poland, such as tax rates. We’ll also calculate effective tax rates and the optimal asset allocation for her portfolio.

Code

portfolio <- create_portfolio_template()

portfolio$accounts$taxable       <- c(0, 1000)
portfolio$accounts$taxadvantaged <- c(0, 500)

portfolio$weights$liabilities[1] <- 0.10
portfolio$weights$liabilities[2] <-  1 - portfolio$weights$liabilities[1]

portfolio$weights$human_capital[1] <- 0.10
portfolio$weights$human_capital[2] <-  1 - portfolio$weights$human_capital[1]

portfolio <- 
  portfolio |> 
  calc_effective_tax_rate(
    tax_rate_ltcg            = 0.19,
    tax_rate_ordinary_income = 0.19
  ) 

portfolio <- 
  calc_optimal_asset_allocation(
    household    = household,
    portfolio    = portfolio
  )

We can now display portfolio assumptions and calculation results in the R console.

Code

portfolio

── Portfolio ───────────────────────────────────────────────────────────────────

── Market assumptions ──

── Expected real returns:

# A tibble: 2 × 3
  name                    expected_return standard_deviation
  <chr>                             <dbl>              <dbl>
1 GlobalStocksIndexFund            0.0461               0.15
2 InflationProtectedBonds          0.02                 0

── Correlation matrix:

                        GlobalStocksIndexFund InflationProtectedBonds
GlobalStocksIndexFund                       1                       0
InflationProtectedBonds                     0                       1

── Weights ──

                        human_capital liabilities
GlobalStocksIndexFund             0.1         0.1
InflationProtectedBonds           0.9         0.9

── Accounts ──

# A tibble: 3 × 4
  name                    taxable taxadvantaged total
  <chr>                     <dbl>         <dbl> <dbl>
1 GlobalStocksIndexFund         0             0     0
2 InflationProtectedBonds    1000           500  1500
3 total                      1000           500  1500

── Pre-tax ──

# A tibble: 2 × 7
  name                    turnover income_qualified capital_gains_long_term
  <chr>                      <dbl>            <dbl>                   <dbl>
1 GlobalStocksIndexFund       0.04                0                       1
2 InflationProtectedBonds     0.04                0                       1
  income capital_gains cost_basis
   <dbl>         <dbl>      <dbl>
1      0        0.0461      0.637
2      0        0.02        0.820

── After-tax ──

# A tibble: 2 × 8
  name                    blended_tax_rate_income blended_tax_rate_capital_gains
  <chr>                                     <dbl>                          <dbl>
1 GlobalStocksIndexFund                      0.19                           0.19
2 InflationProtectedBonds                    0.19                           0.19
  preliquidation_aftertax_expected_return capital_gain_taxed
                                    <dbl>              <dbl>
1                                  0.0430               0.96
2                                  0.0185               0.96
  postliquidation_aftertax_expected_return effective_tax_rate
                                     <dbl>              <dbl>
1                                   0.0373              0.191
2                                   0.0156              0.222
  aftertax_standard_deviation
                        <dbl>
1                       0.121
2                       0

── Allocation ──

# A tibble: 2 × 3
  name                    optimal$taxable $taxadvantaged $total current$taxable
  <chr>                             <dbl>          <dbl>  <dbl>           <dbl>
1 GlobalStocksIndexFund             0.667          0.333      1           0    
2 InflationProtectedBonds           0              0          0           0.667
  $taxadvantaged $total
           <dbl>  <dbl>
1          0          0
2          0.333      1

Output is vast. Let’s zero in on the current and optimal allocation, showcasing them together on one plot.

Code

portfolio |> plot_optimal_portfolio()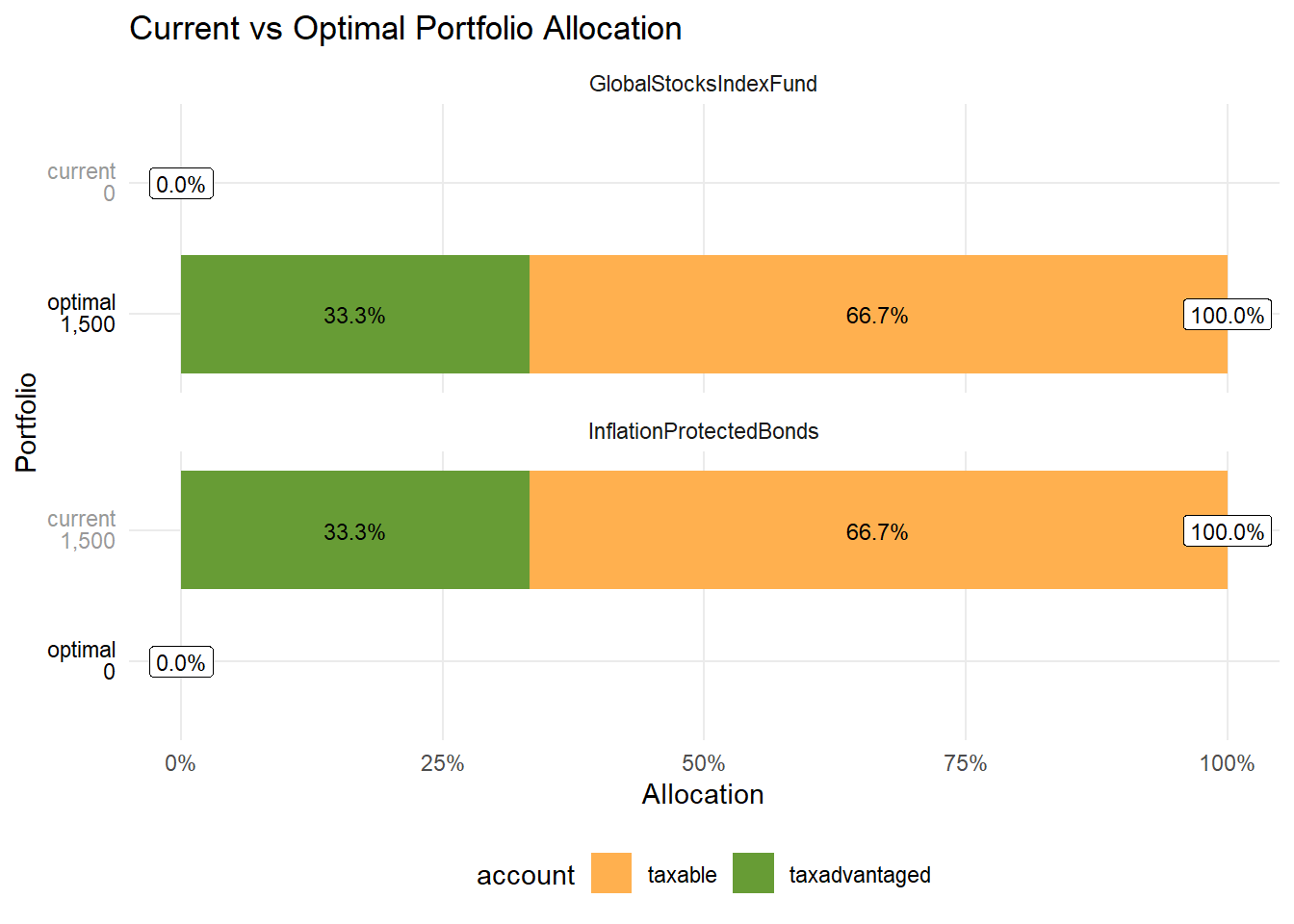

Juliet put all her savings—1’500 PLN—into inflation-protected bonds. But the optimal strategy for her seems to be to move everything into a global stock index fund or ETF, also using tax-advantaged accounts for that. Why? The next sections will reveal more.

Note

The optimal asset allocation here is somewhat similar to the idea of optimal asset allocation based on Merton Share described in this post: How to Determine Our Optimal Asset Allocation?, but in this case, it also takes into account our lifetime human capital and liabilities.

Scenario simulations

Creating Household and Portfolio objects sets the stage to simulate various lifetime scenarios for Juliet.

Simulating basic scenario

Let’s start our simulations with the most basic scenario: we assume Juliet retires at age 60, and her portfolio performance is based on expected market returns.

Code

scenario <- 
  simulate_scenario(
    scenario_id  = glue::glue("Juliet retired at {retirement_start_age}"),
    household = household,
    portfolio = portfolio
  )

── Simulating scenario: Juliet retired at 60

ℹ Current date: 2025-01-01

! Caching is NOT enabled.

→ Simulating a scenario based on expected returns (sample_id==0)

✔ Simulating a scenario based on expected returns (sample_id==0) [1.2s]

Scenario summary

To analyze the simulated data, let’s start by creating a table for Juliet with a scenario snapshot for a given year. Our table should capture values relevant to the current (first) year of our scenario simulation (when Juliet is 20 years old).

Code

scenario |> render_scenario_snapshot(currency = "PLN")

Scenario Summary (2025)
Scenario: Juliet retired at 60

Expected cashflow (monthly)
Income	4 995 PLN
Spending	4 392 PLN
Non-discretionary spending	3 500 PLN
Discretionary spending	892 PLN
Savings	603 PLN
Saving rate	12.1%
Balance sheet
Financial wealth	1 500 PLN
Human capital	1 823 314 PLN
Liabilities	1 574 823 PLN
Net Worth	249 992 PLN
Date: 2025-01-01

Juliet finds actionable insights in the Expected cashflow section. Current assumptions suggest her optimal monthly discretionary spending is 892 PLN. Adding non-discretionary expenses, her total spending reaches 4’392 PLN. She needs to save monthly 603 PLN and invest it in her optimal portfolio.

Juliet’s balance sheet summary reveals the present values of three capital types:

Financial capital: current value of portfolio assets
Human capital: present value of future income streams (salary and pension)
Liabilities: present value of future non-discretionary spending

Her net worth, calculated as the sum of financial and human capital minus liabilities, shows a positive value. This means her net worth could support discretionary spending. Although her financial assets are modest, her human capital—projected future income—offsets her life-time liabilities.

Juliet discovered the essential values from the scenario snapshot table. Let’s see how these values evolve over time.

Plotting expected cash streams

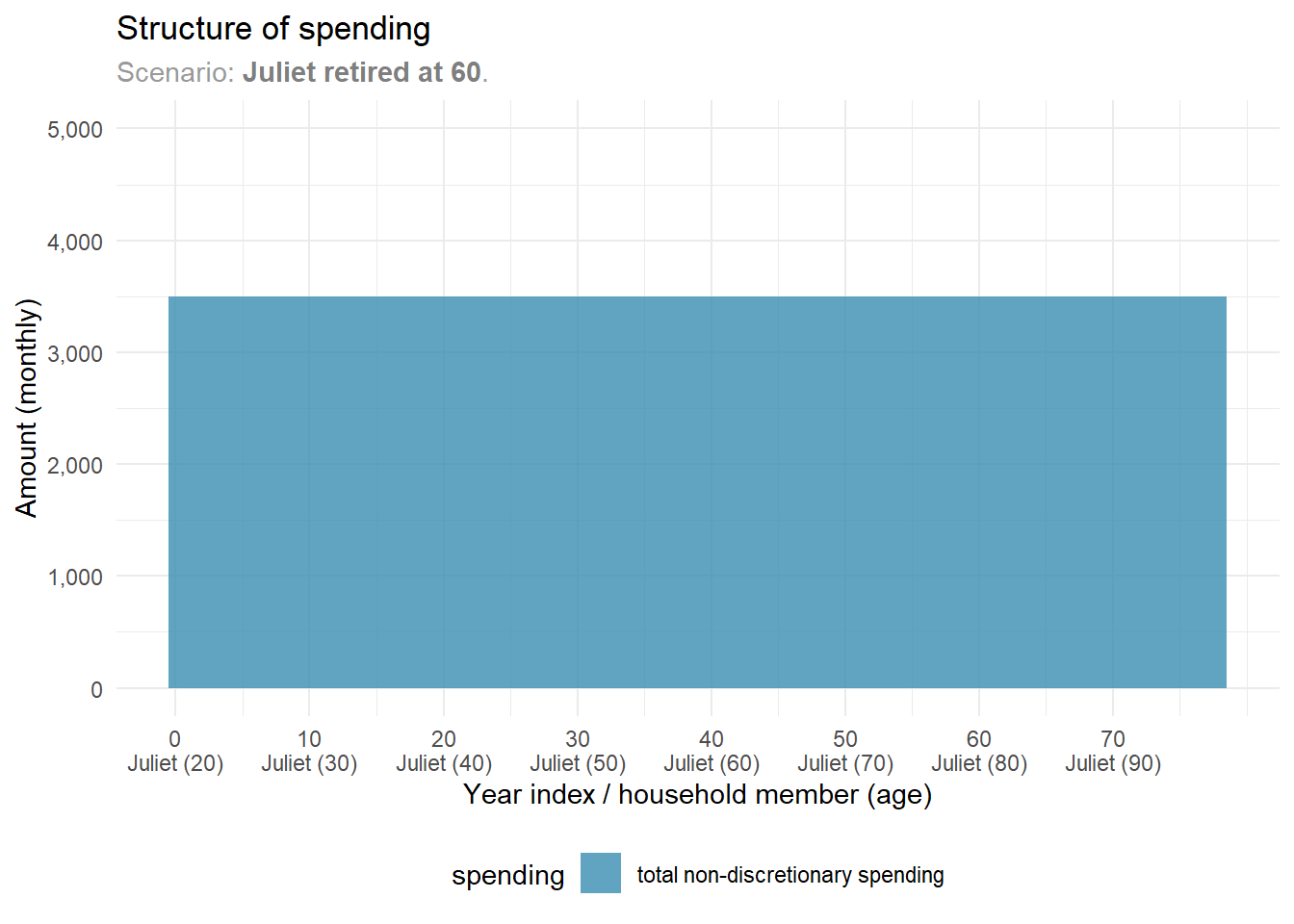
Let’s dive into Juliet’s future income and spending. We’ll start with her anticipated non-discretionary spending. This analysis is straightforward, as she has a single, consistent spending stream. It’s 3,500 PLN, adjusted for inflation, and remains steady over time.

Code

y_limits <- c(NA, 5000)

scenario |> 
  plot_future_spending(
    period   = "monthly", 
    type     = "non-discretionary", 
    y_limits = y_limits
  )

Let’s consider Juliet’s future expected income.

Code

scenario |> 
  plot_future_income(
    period   = "monthly", 
    y_limits = y_limits
  )

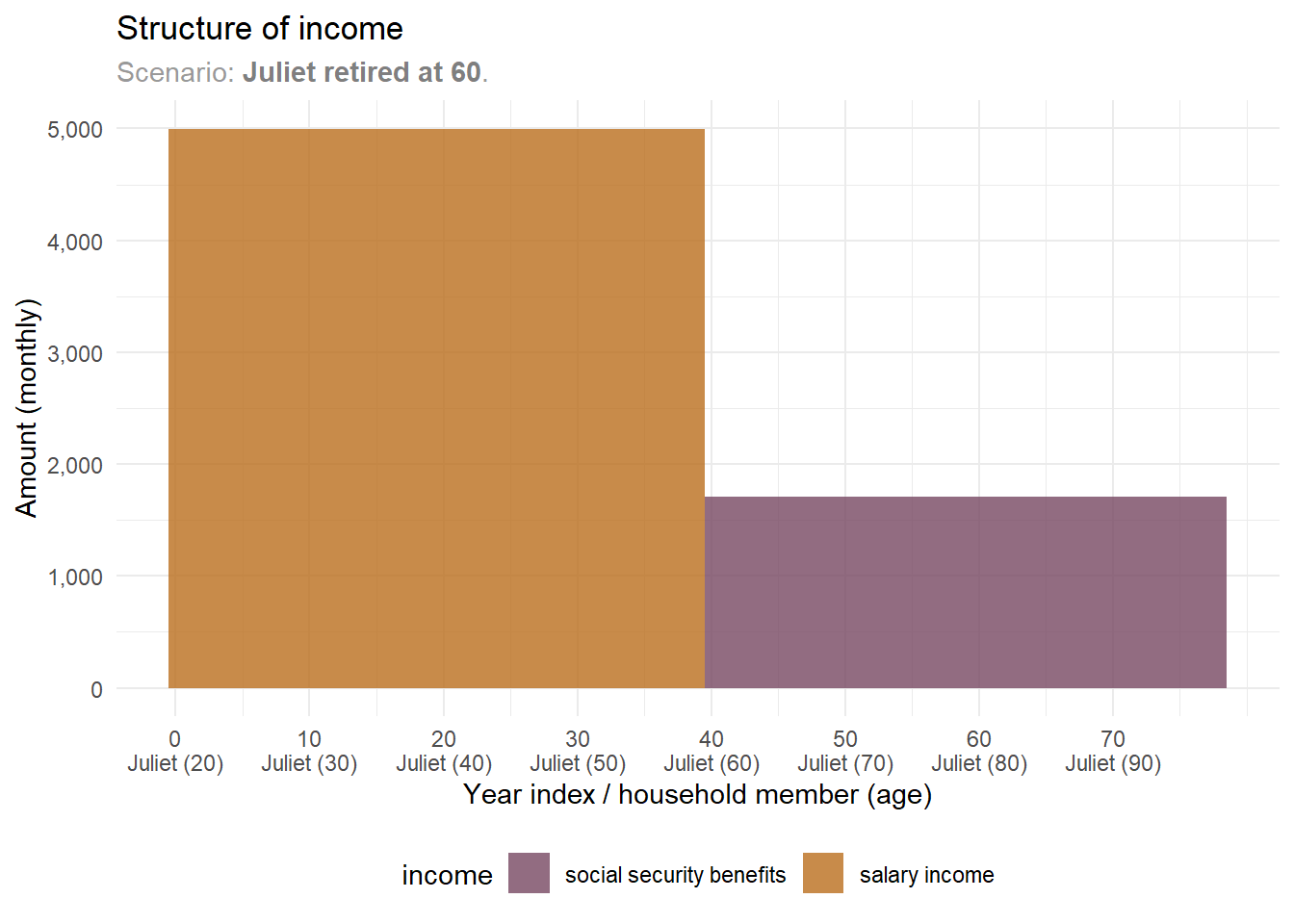
Her income includes two streams: salary and social security benefits. The salary stops when she retires at age 60. At that point, social security benefits kick in, as 60 is the earliest age women in Poland can claim. Currently, Juliet plans to start these benefits right after retiring.

We analyzed income and essential expenses. With this understanding, we can chart Juliet’s expected spending—discretionary and non-discretionary.

Code

scenario |> 
  plot_future_spending(
    period = "monthly",  
    discretionary_spending_position = "top", 
    y_limits = y_limits
  )

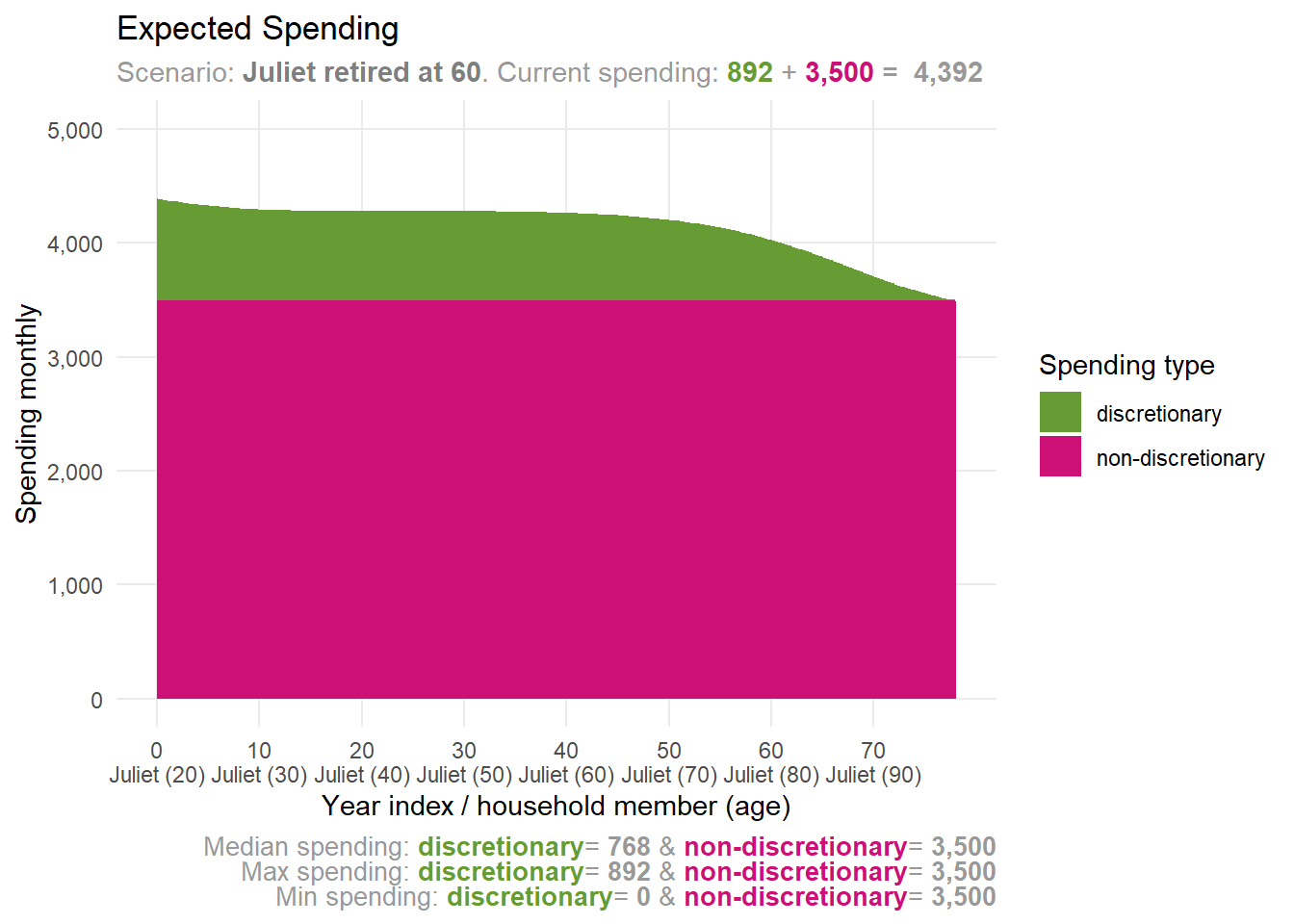
We’ve added discretionary spending on top of the non-discretionary spending plot. It starts at 892 PLN per month in the first year and then fluctuates. Why?

Several reasons: Discretionary spending hits zero as the chance of being alive drops. Meanwhile, Juliet’s household defaults to certain consumption preferences, showing a mix of consumption impatience and desire for smooth consumption. Each of these preferences shapes how discretionary spending changes over time. We are using some reasonable defaults here, but they can be adjusted to match Juliet’s preferences (Idzorek and Kaplan 2024, 17–20). We will discuss how to adjust these preferences in the later blog posts.

Right now, Juliet feels good about her future discretionary spending plans. She’s happy with the current setup, allowing her to indulge a bit more sooner rather than later.

Caution

Juliet’s savings are invested via both taxable and tax-advantaged accounts. Therefore, her spending should be seen as pre-tax. If she plans to cover her expenses with capital gains from taxable accounts, taxes need to be paid first. This means her true available spending will be lower.

Plotting expected saving rates

Juliet wonders if her saving rate will remain steady, rise, or fall over time.

Code

scenario |> plot_future_saving_rates()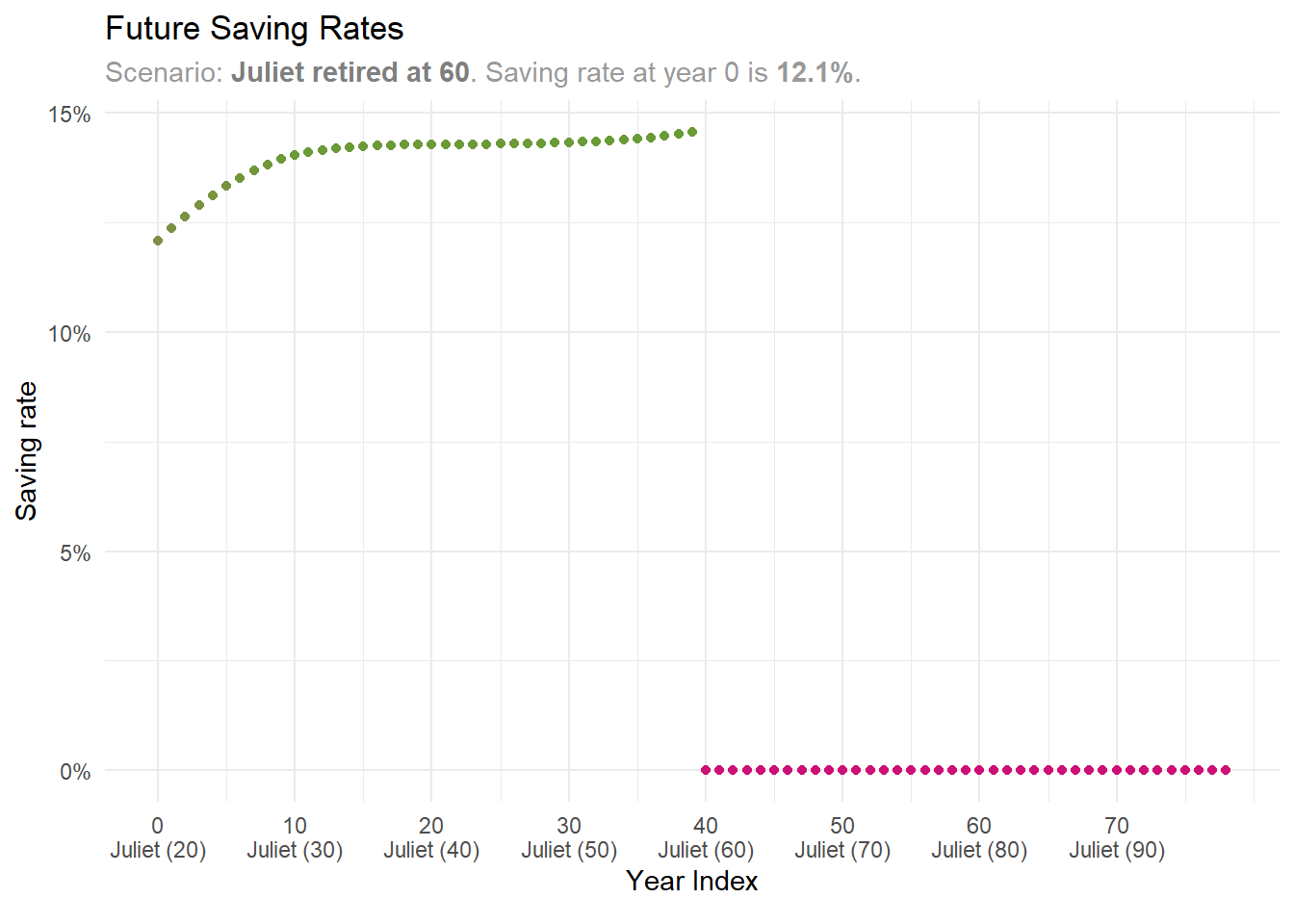

Juliet’s saving rates hover around 12% but are not flat. They stay relatively stable because her income and necessary spending remain steady. The key insight for Juliet is that her current saving rate isn’t permanent; it will likely increase over time as Juliet prefers to spend on non-discretionary items a bit more in the nearest future.

Plotting expected evolution of different capital types

Juliet’s net worth is shaped by her human and financial capital, along with her liabilities. We can illustrate for Juliet how these elements are expected to change over time.

Code

scenario |> plot_expected_capital()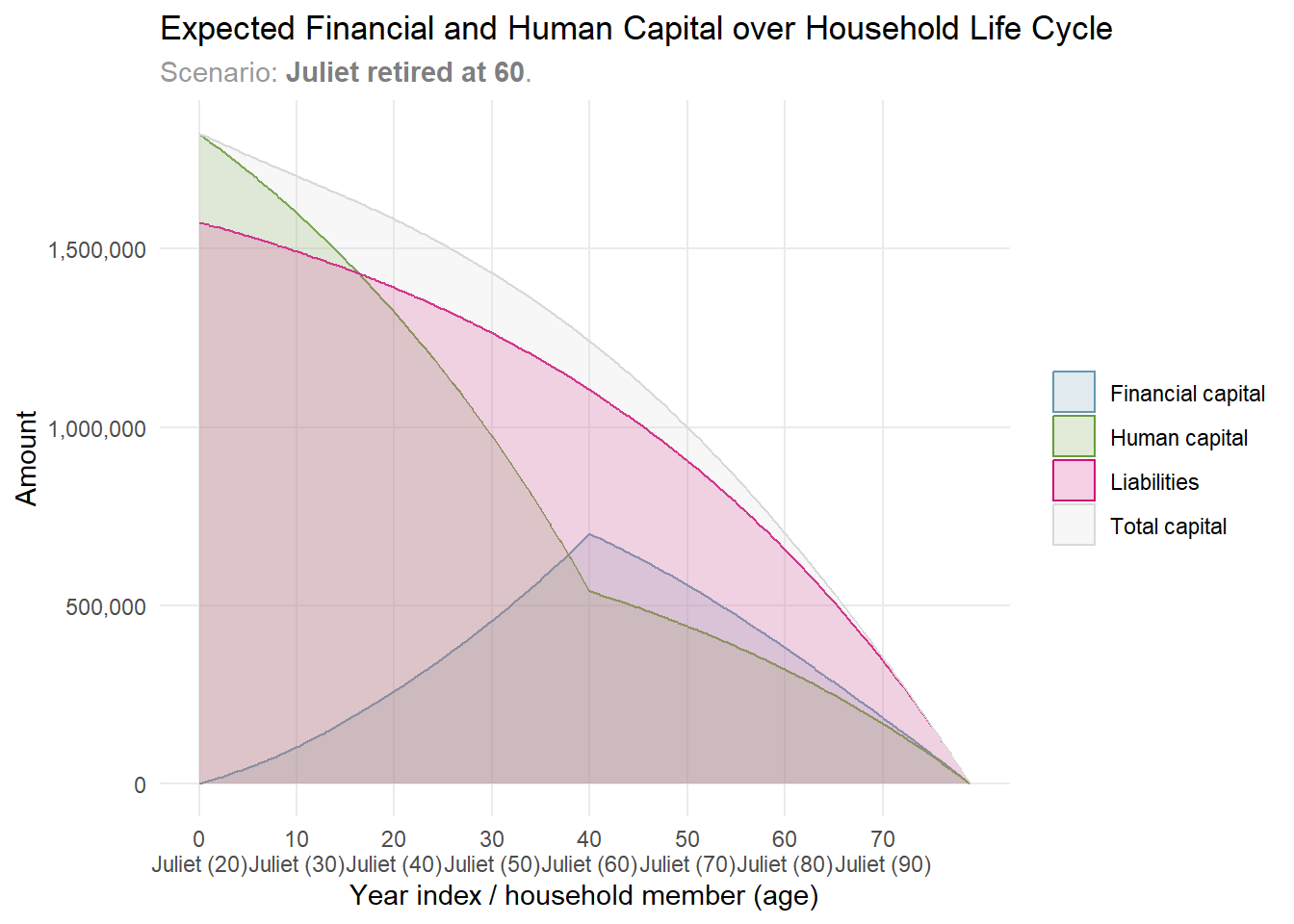

Juliet sees her human capital gradually transform into financial capital, covering both non-discretionary and discretionary expenses.

Simulating basic scenario with Monte Carlo sampling

We’ve been looking at Juliet’s expected scenario, based on anticipated returns for her portfolio. But Juliet is aware that market returns carry uncertainty. Even with a fixed expected value and volatility, the order of those returns can impact Juliet’s finances negatively. This is known as the risk of sequence of returns.

Tip

Read more about the risk of sequence of returns in this section: Why is it important to account for the uncertainty of portfolio returns?

To address this, we can re-simulate Juliet’s scenario. We’ll generate not only the expected returns but also 500 Monte Carlo samples with varied sequences of random returns.

Code

scenario <- 
  simulate_scenario(
    household    = household,
    portfolio    = portfolio,
    scenario_id  = glue::glue(
      "Juliet retired at {retirement_start_age}"
    ),
    monte_carlo_samples = 500,
    seed                = 1234,
    use_cache           = TRUE,
    auto_parallel       = TRUE
  )

── Simulating scenario: Juliet retired at 60

ℹ Current date: 2025-01-01

ℹ Setting random seed to 1234

ℹ Generating random seeds for Monte Carlo samples

ℹ Auto-parallelization enabled with 16 workers.

ℹ Caching is enabled!

→ Simulating a scenario based on expected returns (sample_id==0)

✔ Simulating a scenario based on expected returns (sample_id==0) [1.4s]

→ Simulating 500 Monte Carlo samples

✔ Simulating 500 Monte Carlo samples [3m 26.5s]

Let’s revisit Juliet’s future discretionary spending. This time, we’ll compare her spending based on expected portfolio returns with spending predictions from various Monte Carlo simulations of potential return sequences.

Code

scenario |> plot_future_spending("monthly", "discretionary")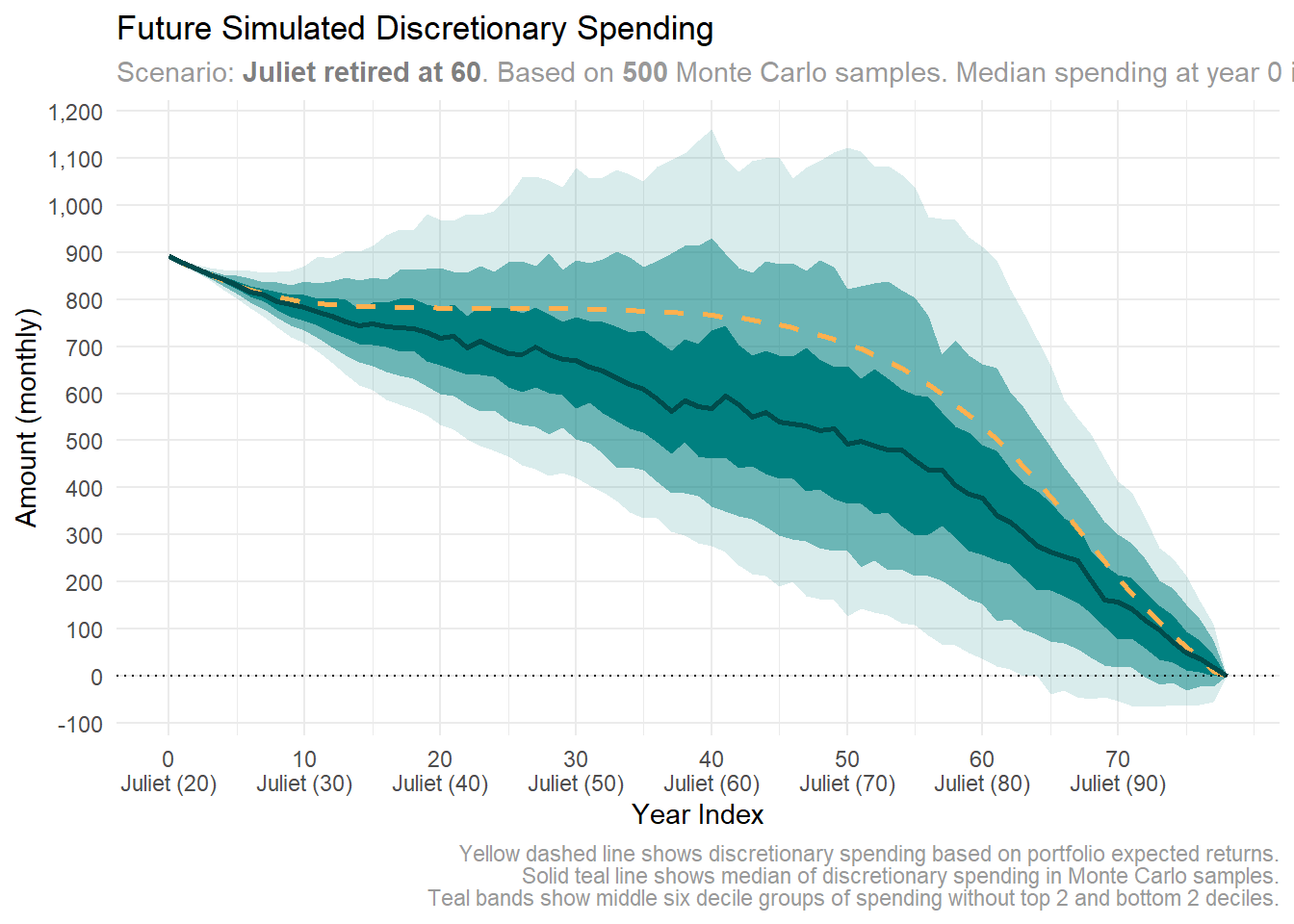

Juliet notices her discretionary spending shifts with portfolio returns, as shown in the plot. The median spending, marked by a solid dark teal line, drops faster than the expected spending, illustrated by a dashed yellow line. Yet, it remains above 500 PLN most of the time—sufficient in Juliet’s view.

If returns are unfavorable, Juliet can adapt. She might boost her savings, trim non-essential expenses, consider retiring later, or seek ways to increase her disposable income.

One more look at possible future saving rates

Juliet noticed that her future savings rate hovers below 15% when her portfolio sees expected returns. But how might these rates shift when averaged across multiple Monte Carlo samples with varying return sequences?

Code

scenario |> plot_future_saving_rates()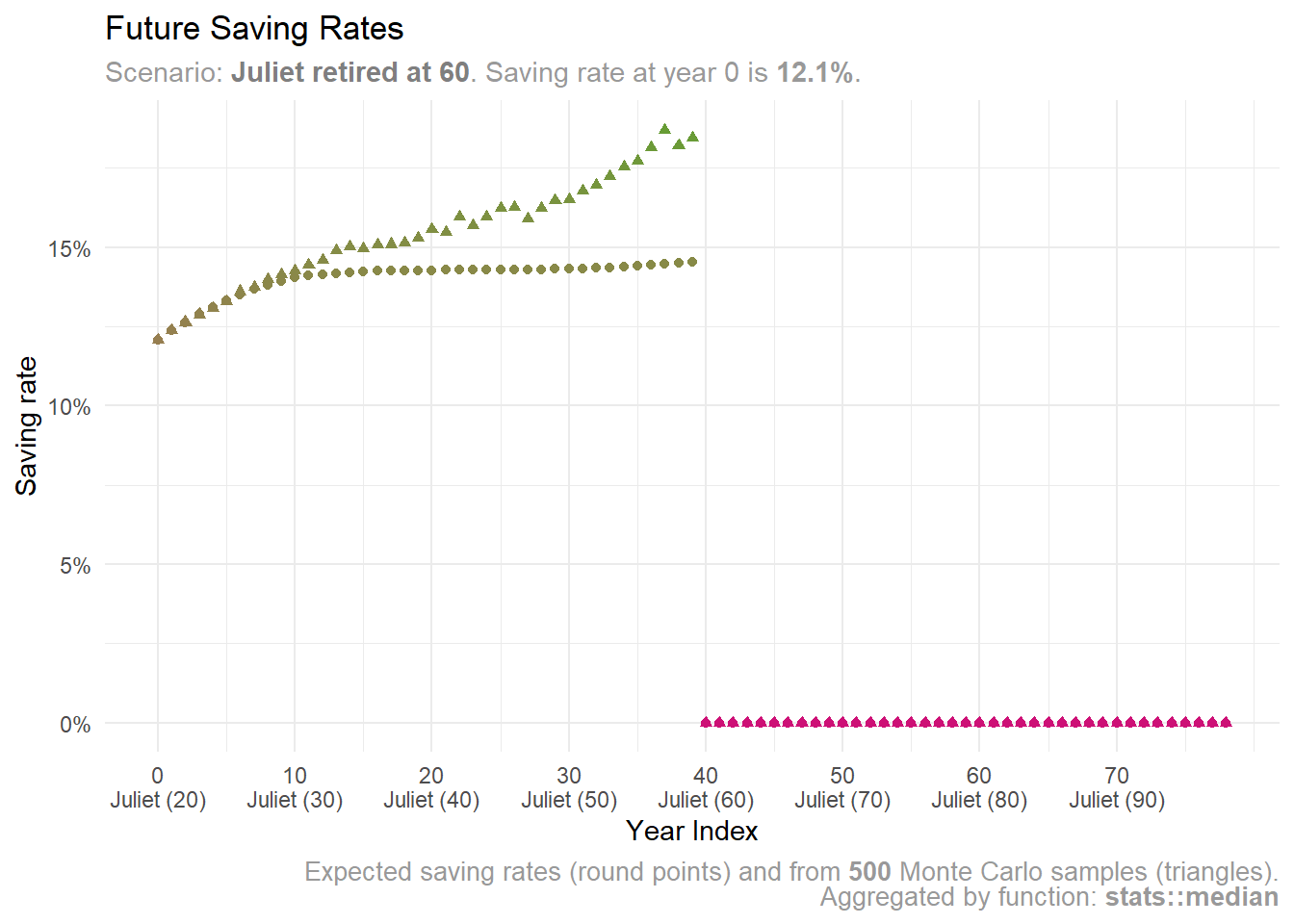

Triangles on the plot display median saving rates from all Monte Carlo samples. Juliet notices they’re rising over time, potentially exceeding 15% due to unfavorable portfolio sequence of returns.

If the worst-case scenarios unfolds, Juliet may need to adapt significantly. She might decide to retire later. Fortunately, she still has time to make that decision. For now, she can wait and assess the sequence of returns as they come, then make the best choice based on her current knowledge and future expectations.

Simulating multiple what-if scenarios

Juliet wonders, what if she changes her retirement age? Can she retire a few years early and still maintain her lifestyle? Or, if she enjoys her work, could she continue longer and have more funds for her dreams?

Let’s create a set of parameters to explore Juliet’s options. We’ll examine retirement starting at ages 50, 55, 60, 65, and 70.

Code

scenarios_parameters <- 
  tibble::tibble(
    member    = "Juliet",
    event     = "retirement",
    start_age = seq(50, 70, by = 5),
    years     = Inf,
    end_age   = Inf
  ) |> 
  dplyr::mutate(
    scenario_id = paste0(substr(member, 1, 1), "-", start_age) 
  ) |> 
  tidyr::nest(events = -scenario_id) 

scenarios_parameters |> 
  tidyr::unnest(events) |> 
  print()

# A tibble: 5 × 6
  scenario_id member event      start_age years end_age
  <chr>       <chr>  <chr>          <dbl> <dbl>   <dbl>
1 J-50        Juliet retirement        50   Inf     Inf
2 J-55        Juliet retirement        55   Inf     Inf
3 J-60        Juliet retirement        60   Inf     Inf
4 J-65        Juliet retirement        65   Inf     Inf
5 J-70        Juliet retirement        70   Inf     Inf

Code

scenarios <- 
  simulate_scenarios(
    scenarios_parameters = scenarios_parameters,
    household            = household,
    portfolio            = portfolio,
    use_cache            = TRUE,
    seeds                = 1234
  )

After simulating multiple scenarios, let’s compare metrics for Juliet’s what-if scenarios on one plot.

Code

scenarios |> plot_scenarios("monthly")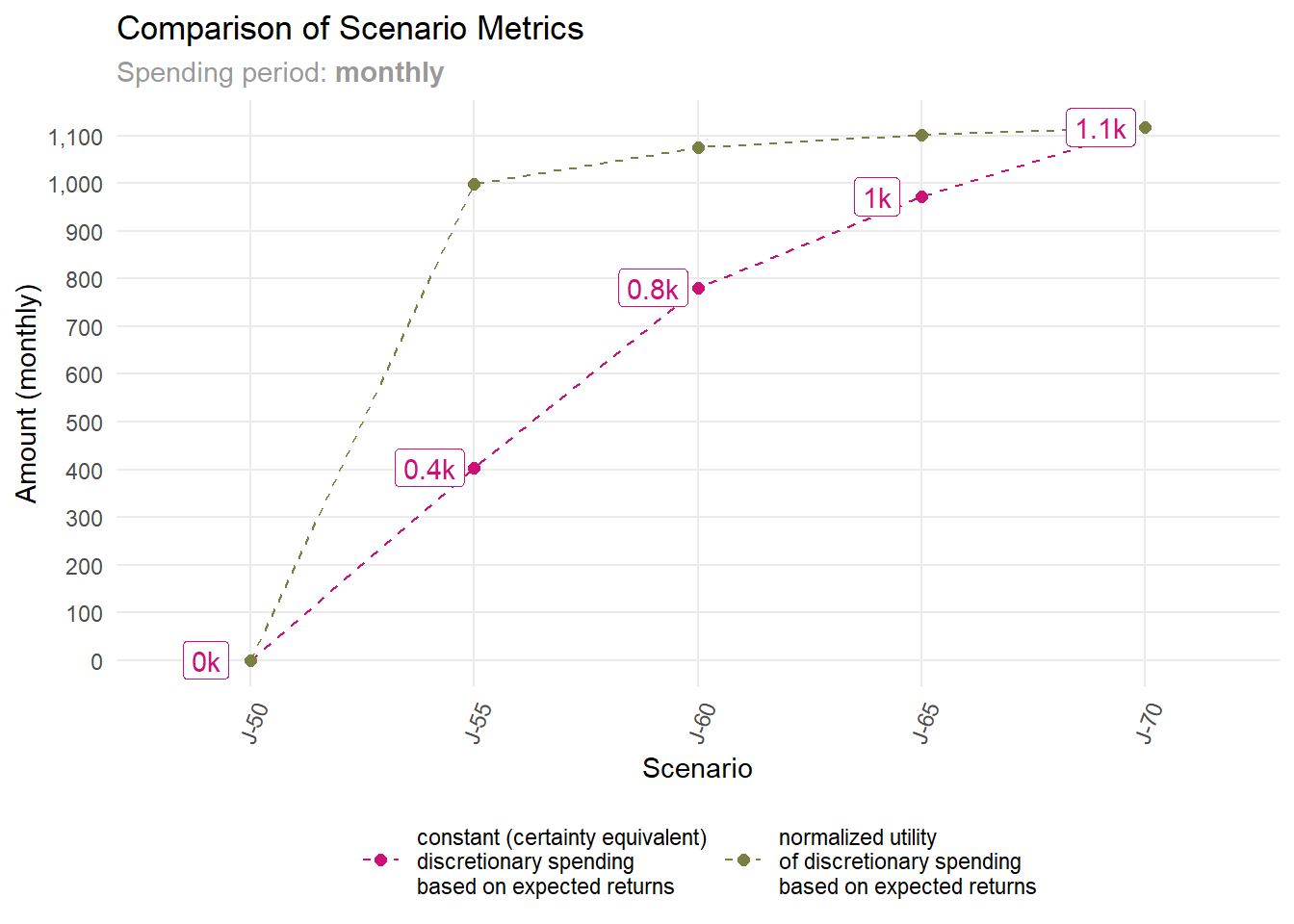

What this plot shows us? A key takeaway is that Juliet should consider scenarios offering notable metric gains.

Take retiring at 50, for example. In the “J-50” scenario (Juliet retiring at 50), her constant discretionary spending⁶ and normalized utility drop to zero. This means she’d lack enough capital for her expenses.

Now, consider retiring at 55. The “J-55” scenario shows a leap to nearly 400 PLN in constant discretionary spending, significantly boosting its utility.

What happens if she retires at 60, under the “J-60” scenario? Constant discretionary spending rises to around 800 PLN, but the utility gain isn’t as pronounced.

While later retirement slightly boosts discretionary spending utility, it still raises constant discretionary spending amount, though also at a slower rate.

Juliet sees 60 as her target retirement age. Yet, she’s curious about shifting the timeline. What if she retires five years earlier or later?

Simulating multiple what-if scenarios with Monte Carlo sampling

Juliet now wants to concentrate on two scenarios she finds most intriguing: retiring at the age of 55 or 65. This time, we plan to generate Monte Carlo samples to conduct a similar analysis to the one we did for the basic scenario (Juliet retiring at 60 years old). This will help us examine how the sequence of risk returns might impact these scenarios differently.

Code

scenarios_parameters <- 
  tibble::tibble(
    member    = "Juliet",
    event     = "retirement",
    start_age = c(55, 65),
    years     = Inf,
    end_age   = Inf
  ) |> 
  dplyr::mutate(
    scenario_id = paste0(substr(member, 1, 1), "-", start_age) 
  ) |> 
  tidyr::nest(events = -scenario_id) 

scenarios <- 
  simulate_scenarios(
    scenarios_parameters = scenarios_parameters,
    household            = household,
    portfolio            = portfolio,
    monte_carlo_samples  = 200,
    use_cache            = TRUE,
    auto_parallel        = TRUE,
    seeds                = 1234
  )

Let’s compare Juliet’s what-if scenarios. We’ll begin with differences in future discretionary spending.

Discretionary spending vs retirement year

Juliet wonders how retiring at 55 might affect her discretionary spending.

Code

y_limits <- c(NA, 1500)
scenarios |> 
  dplyr::filter(scenario_id == "J-55") |>
  plot_future_spending("monthly", "discretionary", y_limits = y_limits)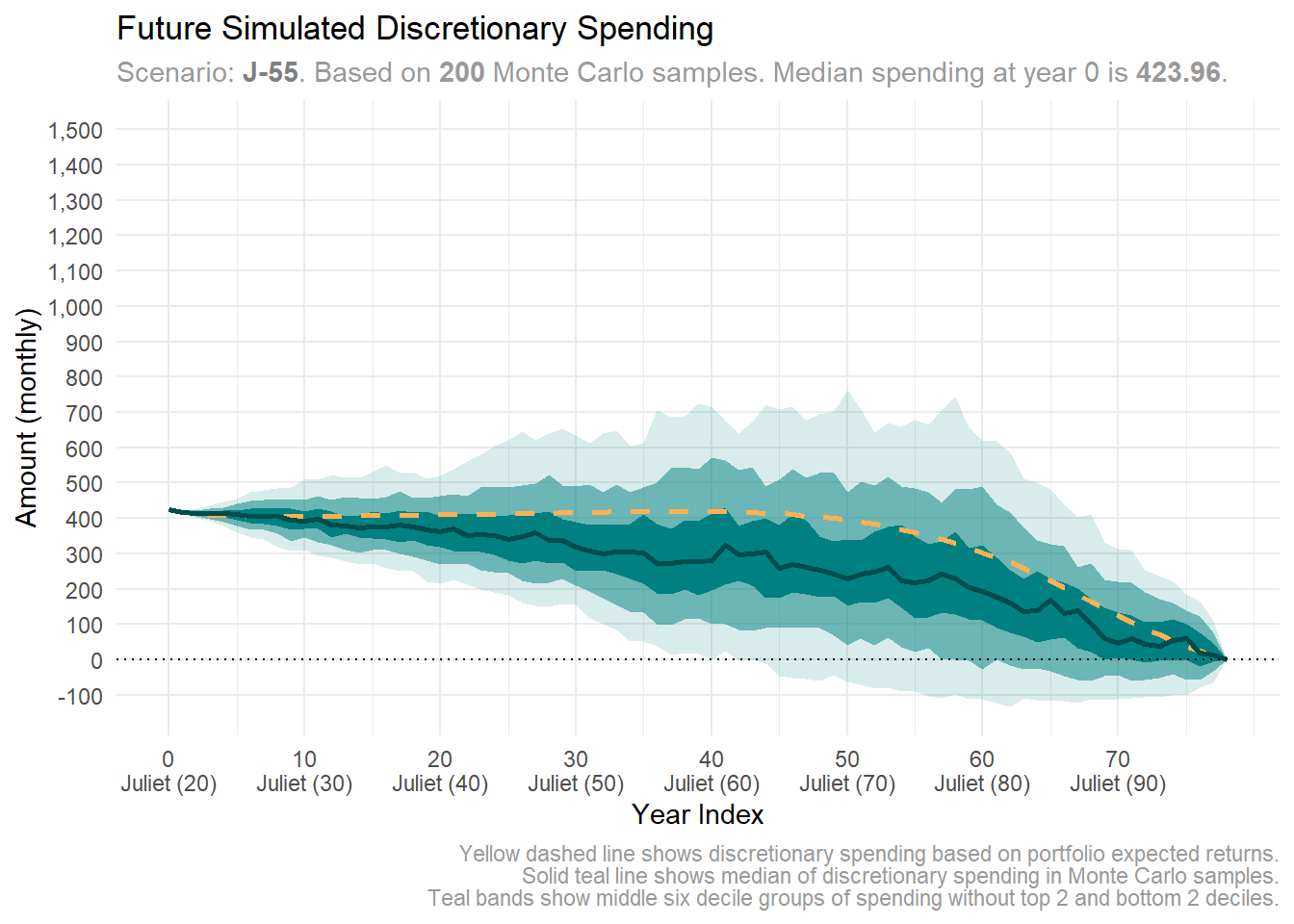

Juliet’s early retirement plan requires her to cut discretionary spending to 423 PLN. There’s also a heightened risk of depleting her capital if returns falter.

She’s considering now waiting until the age of 65 to retire. Could this boost her future spending potential?

Code

scenarios |> 
  dplyr::filter(scenario_id == "J-65") |>
  plot_future_spending("monthly", "discretionary", y_limits = y_limits)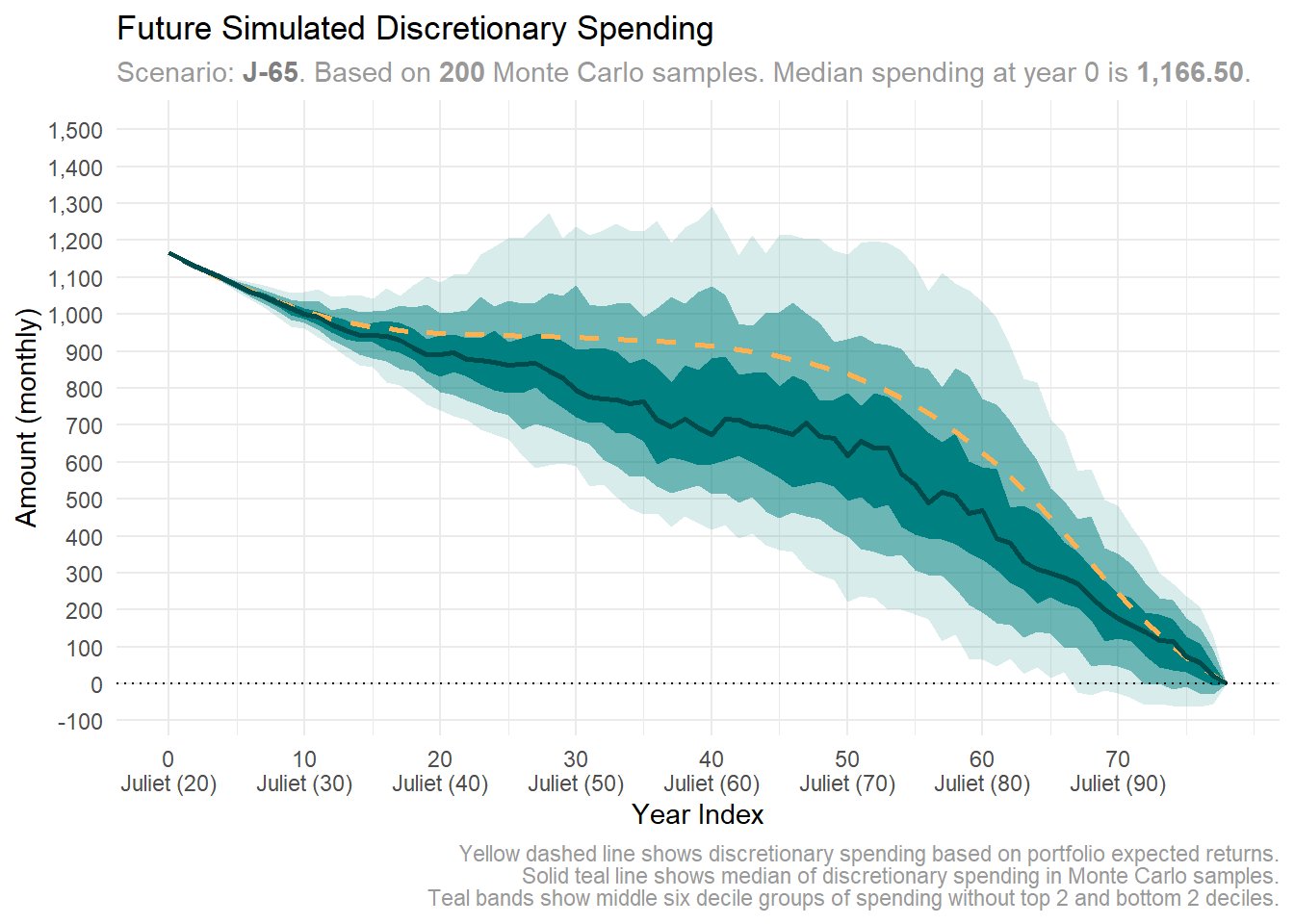

If Juliet retires at 65, she can begin spending 1,166 PLN on discretionary items. Even with less favorable returns, she likely has enough capital to cover additional discretionary spending in the hundreds.

How might these scenarios affect Juliet’s future saving rate?

Saving rates vs retirement year

Juliet wonders how her saving rates would look if she retires at various ages.

Code

y_limits <- c(NA, 0.25)

scenarios |> 
  dplyr::filter(scenario_id == "J-55") |>
  plot_future_saving_rates(y_limits = y_limits)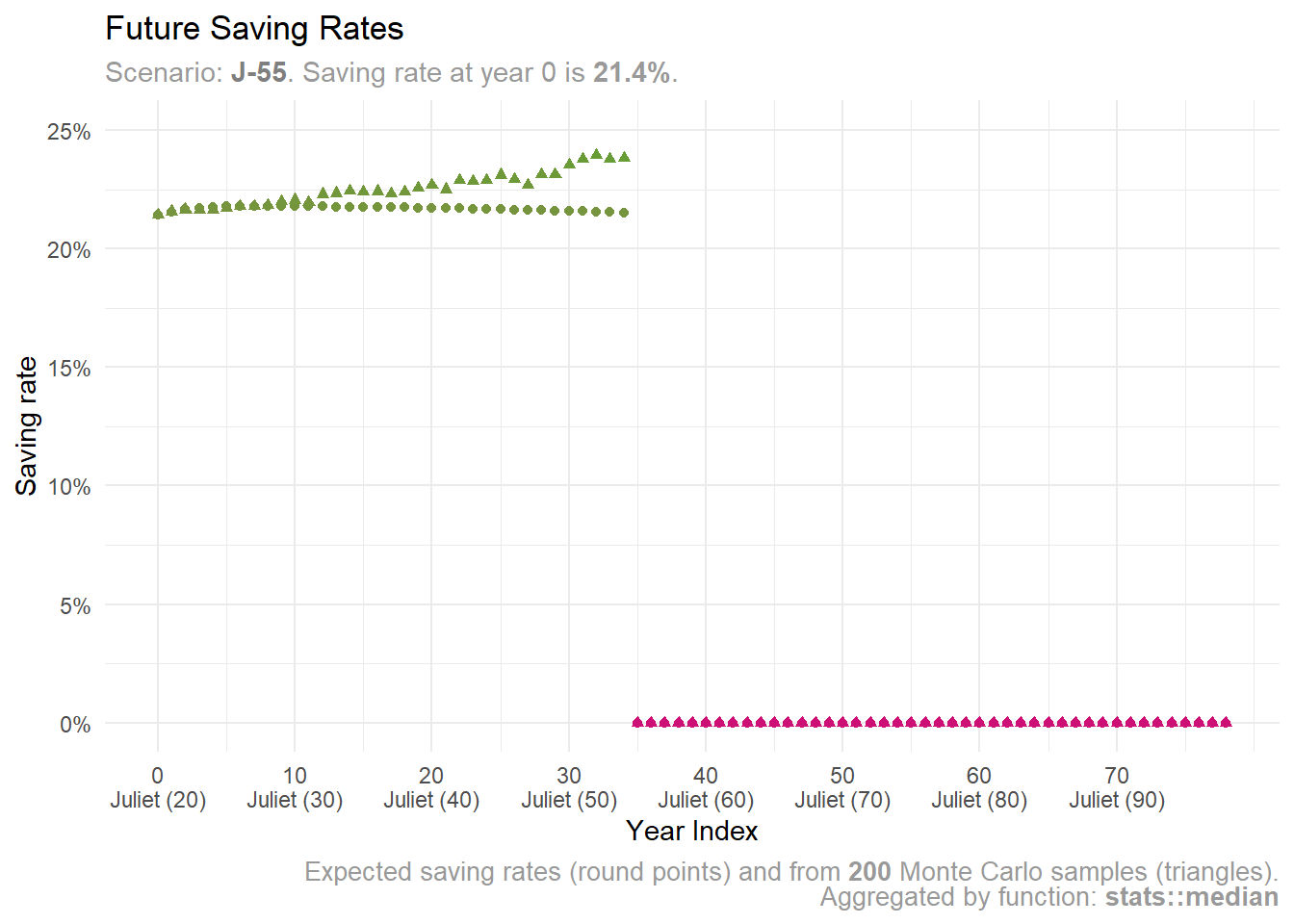

Juliet realizes she needs to save more—over 20%—if she wants to retire early at 55.

Code

scenarios |> 
  dplyr::filter(scenario_id == "J-65") |>
  plot_future_saving_rates(y_limits = y_limits)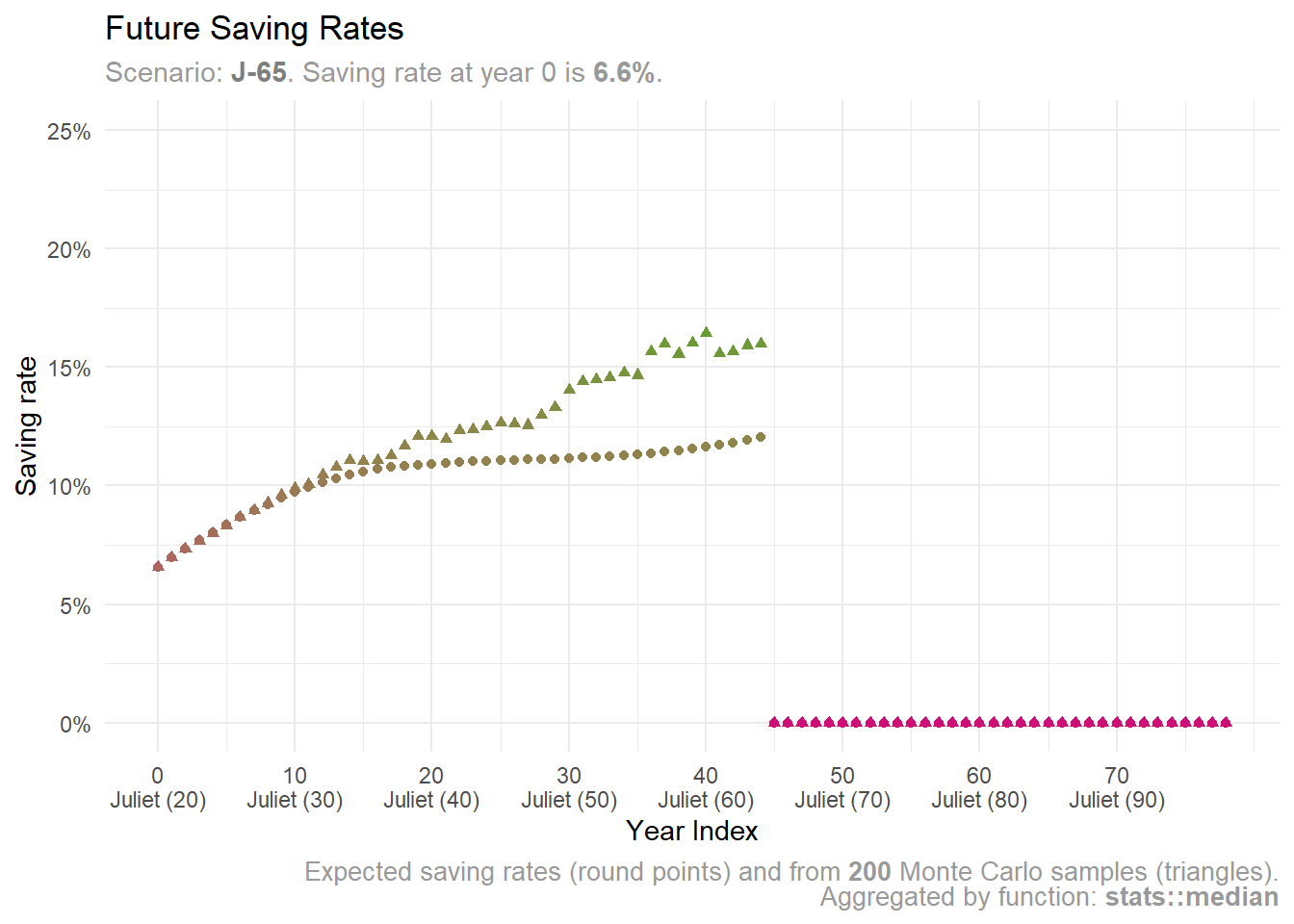

If Juliet retires at 65, she might need to save less—under 10%. However, she may need to boost savings if return rates aren’t favorable.

Expected asset allocation vs retirement year

Juliet’s final focus is on tracking how her optimal asset allocation changes across various retirement scenarios.

Code

scenarios |> 
  dplyr::filter(scenario_id == "J-55") |>
  plot_expected_allocation()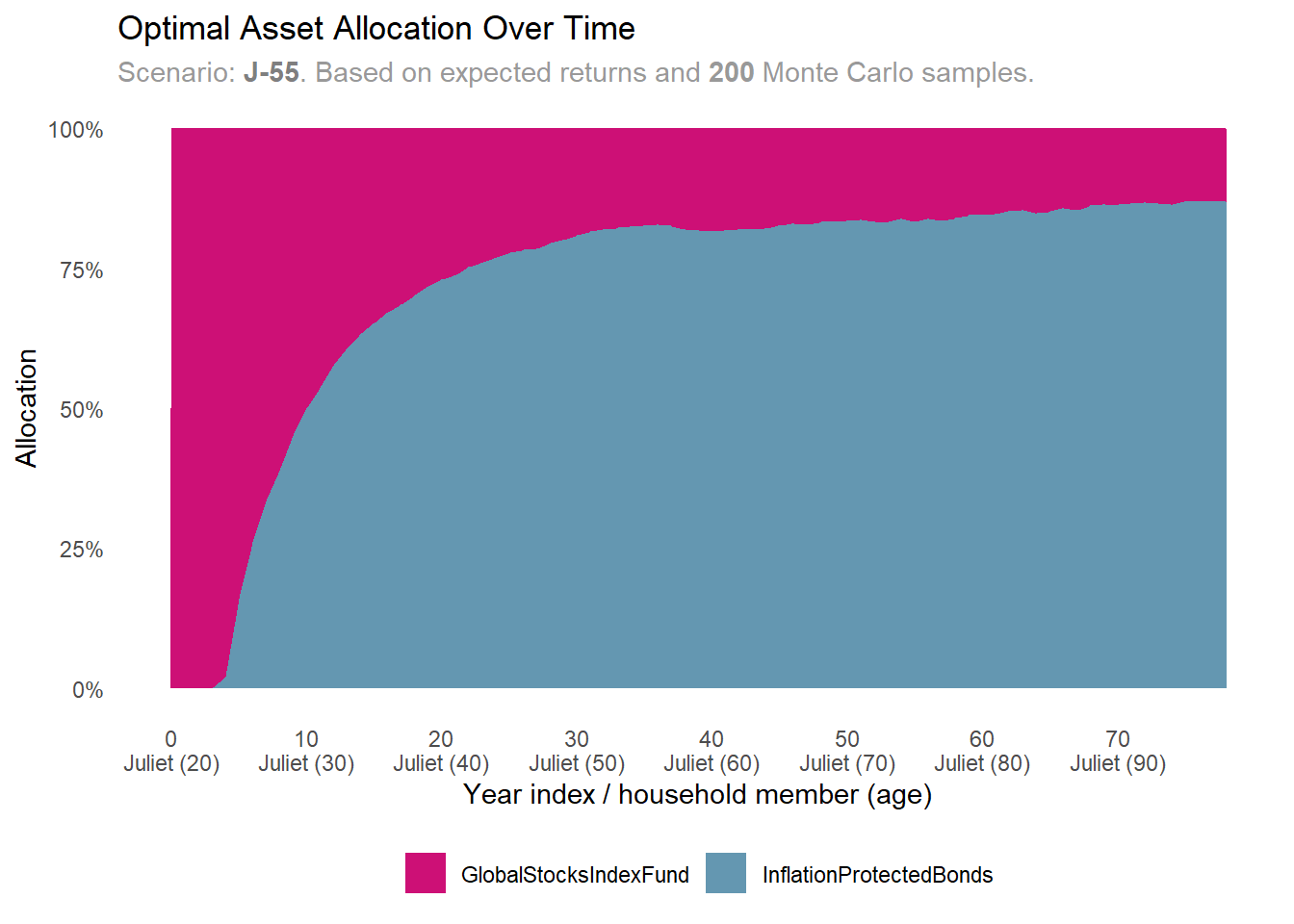

Code

scenarios |> 
  dplyr::filter(scenario_id == "J-65") |>
  plot_expected_allocation()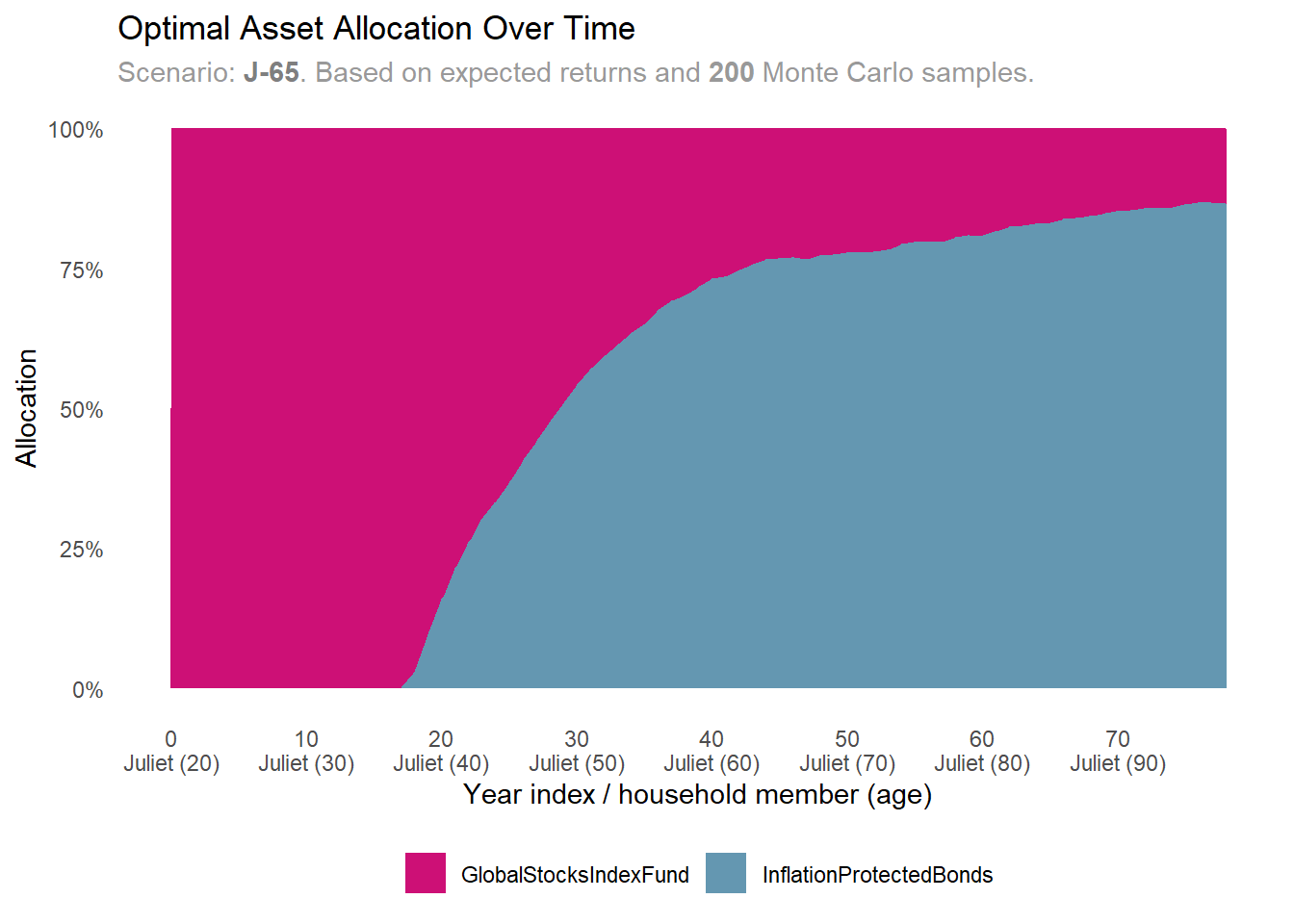

In both retirement scenarios, the model advises Juliet to invest all her financial capital in stocks. This makes sense because her small financial capital is offset by significant bond-like human capital.

As time progresses, the model recommends moving towards bonds in both scenarios. However, in the later retirement scenario, the shift to stocks occurs later than in the earlier one. This is because Juliet plans to work longer, maintaining a larger human capital that she will convert into financial capital over an extended period.

Possible extensions

There are several ways in which Juliet can decide to extend the lifecycle model and simulations:

We’re using two asset types: the risky asset (stocks) and the safe asset (bonds). Our package supports various assets with specific traits, though for most, it’s likely overkill. Leveraging these two asset classes offers a straightforward, effective approach we endorse, aligning with authors such as (Haghani and White 2023) and (Ibbotson et al. 2007).
We use default market assumptions and Poland-specific tax rates. To adapt the model for other countries, update or tailor these elements. You can customize those parameters entirely since the portfolio object functions as an editable data frame, with each asset represented by a single row.
We’re modeling two income streams for Juliet—her salary and social security benefits—and one non-discretionary spending stream. This setup isn’t set in stone. You can tweak it to reflect various income and spending streams as Juliet’s life events unfold.
We’ve predicted two key moments in Juliet’s life: retirement and claiming social security benefits. We could also consider other significant events, such as relocating, marriage, having children, or landing a promotion with a raise. Each of these events might have related changes to Juliet’s income and spending streams.
We’ve based Juliet’s life expectancy on the average for women in Poland. However, this can be adjusted to match her personal life expectancy. For instance, if her parents enjoy long lives, she might anticipate a longer lifespan for herself (and tweak the Gompertz parameters).
Juliet’s household settings use preset values for preferences like consumption impatience, smooth spending, and risk tolerance. You can adjust these to match Juliet’s preferences—for instance, if she wants to spend more early in life and less later, or vice versa.
Juliet plans to claim the minimum social security benefits as early as possible during retirement. It’s worth evaluating if delaying her claim could offer more advantages. The next versions of the package will include custom functions to dynamically calculate income streams based on events like age when you begin claiming social security benefits.

When to claim social security pension?

We assumed Juliet will only claim the minimum social security benefits at retirement. That may be too pessimistic. Even if the average pension replacement rate for young people like Juliet in Poland might be around 40% (OECD 2023, 53–54), Juliet could still receive roughly 2,000 PLN per month at age 60 in today’s terms. That’s a bit more than the current minimum social security benefits (1,710).

Moreover, Juliet’s social security pension will grow if she waits before claiming it. Delaying each year boosts her pension by 8-10% ⁷. Waiting for 10 years, until age 70, could increase Juliet’s pension to 4,000 PLN or more.

Should Juliet delay claiming Social Security? That is a topic for another post. But it’s worth considering in her financial model. Social Security works like an inflation-indexed annuity from the recipient’s perspective (Ibbotson et al. 2007, vii). This makes it crucial insurance against outliving ones savings.

Conclusion

Juliet thrives solo in a single-person household in a bustling Polish city. She navigates life independently, whether or not Romeo is by her side, or if they haven’t crossed paths, or perhaps they did, but he wasn’t quite right for her. Our simulations suggest this single-person household scenario is realistic for Juliet.

Juliet bases her decisions on current assumptions about the future market and a median salary that aligns with inflation. The future is uncertain, which means these assumptions might shift. However, decisions must be made today, rooted in what seems most reasonable right now.

When the future looks bleak, Juliet will adapt. She might ramp up her savings, cut unnecessary costs, think about retiring later, or find ways to boost her income—like taking on part-time work or seizing business opportunities. But if the future shines bright, she could decide to enjoy more discretionary spending, retire earlier, or even do both.

You can see that with the household lifecycle framework you can quite quickly reach an optimal (or near-optimal) recommendation tailored to your own specific situation at a given moment.

In future posts, we’ll explore scenarios where Juliet and Romeo choose to spend their life together. Our simulation will include diverse income sources, multiple necessary expenses, and varied life expectancy assumptions. Eventually, we’ll even factor in children.

Tip

Enjoyed this post? Share it with others who might find it interesting. Subscribe to our newsletter to stay updated. Thanks for reading!

References

CFP Board, ed. 2015. Financial Planning Competency Handbook. 2nd ed. Hoboken, NJ: John Wiley & Sons. https://doi.org/10.1002/9781119642473.

Haghani, Victor, and James White. 2023. The Missing Billionaires: A Guide to Better Financial Decisions. Hoboken, New Jersey: John Wiley & Sons, Inc.

Ibbotson, Roger G., Moshe A. Milevsky, Peng Chen, and Kevin X. Zhu. 2007. “Lifetime Financial Advice: Human Capital, Asset Allocation, and Insurance.” Monograph. Research Foundation of CFA Institute. https://rpc.cfainstitute.org/research/foundation/2007/lifetime-financial-advice-human-capital-asset-allocation-and-insurance.

Idzorek, Thomas M., and Paul D. Kaplan. 2024. Lifetime Financial Advice: A Personalized Optimal Multilevel Approach. CFA Institute Research Foundation.

Milevsky, Moshe A. 2012. Are You a Stock or a Bond? Identify Your Own Human Capital for a Secure Financial Future. Updated and Revised. FT Press.

OECD. 2023. Pensions at a Glance 2023: OECD and G20 Indicators. Paris: OECD Publishing. https://doi.org/10.1787/678055dd-en.

Footnotes

Juliet’s expectation for clear advice seems to be in line with the Financial Planning Competency Handbook by the CFP Board: Presenting planning alternatives, while useful in showing a client the many paths available to reach a financial goal, can create decision paralysis among some clients. This is the reason that the planner should conclude with a clear set of recommendations that leave the client in no doubt as to what must be done next (CFP Board 2015, 606). Using life-cycle model, we can recommend Juliet not only one of many alternatives of recommendations, but a single set of recommendations that should be optimal for her (or at lest close to optimal).↩︎
The median salary in Poland in 2024 was 6’842 PLN gross per month, and about 4’995 PLN net per month. See: https://stat.gov.pl/obszary-tematyczne/rynek-pracy/pracujacy-zatrudnieni-wynagrodzenia-koszty-pracy/rozklad-wynagrodzen-w-gospodarce-narodowej-w-listopadzie-2024-r-,32,11.html↩︎
The net minimum social security benefits in Poland in 2025 is 1’878.91 PLN per month gross, which is about 1’709.81 PLN net. See: https://www.gov.pl/web/rodzina/waloryzacja-rent-i-emerytur-w-2025-roku–wzrost-swiadczen-dla-milionow-polakow↩︎
The costs of leaving for a single in a big city in Poland in 2025 were estimated at 4’000 PLN per month. This included also discretionary spending like 450 PLN for cinema tickets, eating out, subscriptions. Based on that we assumed that non-discretionary spending is about 3’500 PLN. See: https://www.bankier.pl/smart/ile-kosztuje-zycie-singla-vs-rodziny-w-2025-budzety-ktore-otwieraja-oczy (in Polish)↩︎
Read more about human capital in (Milevsky 2012), (Ibbotson et al. 2007), and (Idzorek and Kaplan 2024).↩︎
Constant discretionary spending—certainty equivalent constant level of spending that would result in the same lifetime utility as a series of (non-constant) future spending in a given scenario.↩︎
See article (in Polish): https://businessinsider.com.pl/praca/emerytury/emerytura-jak-uzyskac-wyzsze-swiadczenie-ike-ppk-odroczenie-emerytury-prezes-zus/cx88knm. The similar situation is in US, where Social Security payments increase 8 percent for every year after full retirement age that a retiree waits to claim benefits. A retiree who des not take early Social Security benefits may enjoy a benefit up to 30 percent grater than one who receives benefits at the earliest possible age. (CFP Board 2015, 437)↩︎

Citation

BibTeX citation:

@online{wais2025,
  author = {Wais, Kamil and Wais, Olesia},
  title = {Can {Juliet} Manage Without {Romeo?} {How} Much She Should
    Spend, Save, and Invest to Achieve That?},
  date = {2025-07-27},
  url = {https://r4good.academy/en/blog/financial-report-individual-minimal-example/index.en.html},
  langid = {en}
}

For attribution, please cite this work as:

Wais, Kamil, and Olesia Wais. 2025. “Can Juliet Manage Without Romeo? How Much She Should Spend, Save, and Invest to Achieve That?” July 27, 2025. https://r4good.academy/en/blog/financial-report-individual-minimal-example/index.en.html.

--- title: "Can Juliet manage without Romeo? How much she should spend, save, and invest to achieve that?" # TODO: post description and tags description: "You will learn how to quickly get to optimal decisions about discretionary spending and portfolio allocation by simulating scenarios for a single-person household. We will use reasonable defaults to simplify the example, but you can customize them to your own scenarios." author: - "Kamil Wais" - "Olesia Wais" categories: [R4GoodPersonalFinances, R package, RBloggers, personal finance, retirement, life-cycle model, financial planning, financial report] engine: knitr code-overflow: wrap code-fold: show code-link: true code-copy: true # code-tools: false code-tools: true code-block-bg: '#F8F9FA' reading-time: true fig-cap-location: bottom toc: true toc-depth: 9 toc-expand: 1 execute: echo: true output: true freeze: auto editor: source citation: true # draft: true date: "2025-07-27" # date-modified: "2024-12-31" ---  ## Meet Juliet Juliet just turned 20 and is ready to start her adult life. She's landed a stable, well-paid job and her new journey begins. This time, life unfolds without Romeo. Think she can't handle it? You might be surprised. Juliet feels anxious about her future. Each month she have to choose how to balance spending, saving, and investing for what's ahead. She's keen to avoid poor decisions. Juliet seeks clear, rational advice tailored to her needs—**not the generic advice** that's all over the internet. She aims to make **informed, personalized financial choices** that align with her present knowledge and future plans. She needs a clear set of recommendations to know how much to save and how to invest [^recommendations]. [^recommendations]: Juliet's expectation for clear advice seems to be in line with the *Financial Planning Competency Handbook* by the CFP Board: *Presenting planning alternatives, while useful in showing a client the many paths available to reach a financial goal, can create decision paralysis among some clients. This is the reason that the planner should conclude with a clear set of recommendations that leave the client in no doubt as to what must be done next* [@cfpboard2015competency, p.606]. Using life-cycle model, we can recommend Juliet not only one of many alternatives of recommendations, but a single set of recommendations that should be optimal for her (or at lest close to optimal). Let's follow Juliet's example to craft a **straightforward financial report for a single-person household**. We will be using our new `R4GoodPersonalFinances` R package that implements (with our modifications) the theoretical model invented and described in *Lifetime Financial Advice: A Personalized Optimal Multilevel Approach* by Thomas M. Idzorek and Paul D. Kaplan [@LifetimeFinancialAdvice2024]. ### Juliet's assumptions and expectations We aim to explore scenarios that an individual might encounter, based on realistic assumptions about market returns and living expenses in a big Polish city. These scenarios reflect a consistent, median-level income. We focus on income and spending estimates for Poland, using Polish złoty (PLN). However, you can adapt these scenarios to any currency or country-specific factors. ```{r} #| label: monthly income and spending #| output: false #| code-fold: true monthly_income <- 4995 monthly_social_security_benefits <- 1710 monthly_cost_of_living <- 3500 ``` ```{r} #| label: currency formatting #| echo: false #| output: false format_currency_custom <-function(x) { paste0( "**", R4GoodPersonalFinances::format_currency(x, suffix = " PLN", big.mark = "'"), "**" ) } format_currency_custom(monthly_income) ``` Juliet, a 20-year-old young woman that leaves in a big city in Poland, chooses to stay single. She imagines this will be her lifelong path. Juliet has just got a job, so she expects a steady income of `r format_currency_custom(monthly_income)` net salary per month (real / inflation-adjusted). When she retires (at the age of 60 or later) she will receive a pension from Polish social security (*emerytura ZUS*) of `r format_currency_custom(monthly_social_security_benefits)` per month (in today's money and inflation-adjusted). Juliet plans to spend `r format_currency_custom(monthly_cost_of_living)` each month on her basic needs. This covers her essential, non-discretionary expenses. Beyond that, she would like to allocate some funds for discretionary spending – the things that bring her joy. Juliet holds modest savings of `r format_currency_custom(1500)`, already invested in two assets: a global stock ETF and Polish inflation-protected bonds, known as EDO. Juliet aims to apply a lifecycle model to pinpoint her optimal discretionary spending and asset allocation. She also wants to explore how her discretionary spending might shift if she retires at various ages. ## Setting up the technical essentials for the report ### Loading the package ```{r} #| label: R4GoodPersonalFinances R package #| echo: false #| output: false #| eval: false # rstudioapi::restartSession() # devtools::load_all("../R4GoodPersonalFinances") # install.packages("R4GoodPersonalFinances", repos = "https://cran.r-project.org") pak::local_install("../R4GoodPersonalFinances", upgrade = FALSE, ask = FALSE) ``` ```{r} #| label: load the package library(R4GoodPersonalFinances) ``` ```{r} #| label: setting cache directory #| echo: false #| output: false if (interactive()) { set_cache(path = "blog/financial-report-individual-minimal-example/.cache") } else { set_cache() } # reset_cache() ``` ### Setting the date of the report We start with setting one common `current_date` for all analyses in the report. Let's assume that the current date is `2025-01-01`. We could set the `current_date` parameter in each function call, but we can also set it as a global option for the entire R session - like in our example. If we didn't set the `current_date` parameter, it would be set to the current computer date by default. As a result, the report cold not be the same if rendered for different dates. So for reproducibility, we set the `current_date` to this arbitrary date `2025-01-01` for the whole R session. ```{r} #| label: setting current date options("R4GPF.current_date" = "2025-01-01") ``` ## Creating Juliet's household ### Defining the household member First, we need to create an object of `HouseholdMember` class that represents Juliet. ```{r} #| label: create household member object juliet <- HouseholdMember$new( name = "Juliet", birth_date = "2005-01-01" ) juliet ``` Juliet came into this world on January 1, 2005—exactly 20 years before the report's date, January 1, 2025. By default, her maximum age is 100 years. So, her remaining lifespan is 80 years, calculated as maximum age minus current age (100 - 20 = 80). We haven't determined mode and dispersion for the Gompertz model yet, so life expectancy remains unclear. Let's address that now. #### Setting Gompertz parameters for Juliet Let's find Julia's Gompertz parameters: mode and dispersion. We'll calculate these using data from a typical 20-year-old Polish woman and then apply them to Julia. ::: {.callout-tip} Discover why Gompertz parameters matter and how to model them here: [How to model our probability of survival?](https://www.r4good.academy/en/blog/retirement-ruin/index.en.html#how-to-model-our-probability-of-survival) ::: ```{r} #| label: calculating gompertz parameters for Juliet gompertz_parameters <- get_default_gompertz_parameters( age = juliet$calc_age(), country = "Poland", sex = "female" ) juliet$mode <- gompertz_parameters$mode juliet$dispersion <- gompertz_parameters$dispersion juliet$max_age <- gompertz_parameters$max_age juliet ``` We estimate Juliet could live up to `r round(juliet$max_age, 1)` years, with an expected lifespan of about `r round(juliet$calc_life_expectancy(), 1)` years. ### Defining Juliet's household Let's start a household with Juliet. Juliet is the lone member, but she is welcome to add others as needed in the future. ```{r} #| label: creating a household household <- Household$new() household$add_member(juliet) household ``` You can see that we successfully added Juliet to her household. Juliet's household comes with preset preferences. Key ones include: - Consumption impatience. - Smooth consumption. - Risk tolerance. Future posts will explore these preferences in detail and offer tips on customization. For now, let's assume that default values of those preferences are sensible and will work for Juliet well enough. Juliet's lifespan matches that of her household since she's its sole member. You can visualize the lifespans of household members by plotting their age-of-death probability distributions and life expectancy. ```{r} #| label: plotting life expectancy household |> plot_life_expectancy() ``` On the plot, Juliet sees her life expectancy is `r round(juliet$calc_life_expectancy(), 1)` years. She knows this is just an estimate; her actual lifespan could be shorter or longer. **The life-cycle model takes into account all probabilities tied to different lifespans**. She may consider in the future adjusting the Gompertz parameters to match her life expectancy expectations. For now, she's content with the defaults. #### Defining income and spending expectations We need to **define both income and spending in "real" terms** to account for inflation over time. For instance, setting a real income of 1 000 PLN implies it maintains its purchasing power and increases with inflation. This way, years later, you can still buy what 1 000 PLN can buy today. This is a reasonable, though optimistic, expectation for salary and more realistic for inflation-adjusted social security pensions. We need to set **expected annual income and expenses**. If you have a monthly amount, multiply it by 12 for the yearly total. We'll demonstrate next how to define cash flow streams linked to events affecting a household member. In this case, we'll focus on income changes tied to a `retirement` event and Juliet's age. ##### Setting the `retirement` event ```{r} #| label: setting retrirement start age retirement_start_age <- 60 ``` As Juliet expects to retire at the age of `r retirement_start_age` years, we set the `retirement` event to start at this age. We also assume that Juliet will be retired till the end of her life. ```{r} #| label: setting retirement event juliet$set_event("retirement", start_age = retirement_start_age) ``` ##### Setting expected disposable income streams Juliet expects that in her lifetime she will be receiving two income streams: salary income and social security pension income. The income needs to be defined as **net disposable income** - the after-tax income that Juliet can spend on stuff she needs and wants (non-discretionary and discretionary spending). ###### Salary income Juliet is moderately optimistic about her future income. She expects to make `r format_currency_custom(monthly_income)` net salary per month (after taxes). This is coincidentally the **median net salary** in Poland in November 2024[^median_salary]. [^median_salary]: The median salary in Poland in 2024 was **6'842 PLN** gross per month, and about **4'995 PLN** net per month. See: https://stat.gov.pl/obszary-tematyczne/rynek-pracy/pracujacy-zatrudnieni-wynagrodzenia-koszty-pracy/rozklad-wynagrodzen-w-gospodarce-narodowej-w-listopadzie-2024-r-,32,11.html ###### Pension income Juliet also expects to receive a pension from Polish social security (*emerytura ZUS*) of `r format_currency_custom(monthly_social_security_benefits)` per month. This is coincidentally the **net minimum social security pension** in Poland in 2025[^minimal_social_security_benefits]. [^minimal_social_security_benefits]: The net minimum social security benefits in Poland in 2025 is **1'878.91 PLN** per month gross, which is about **1'709.81 PLN** net. See: https://www.gov.pl/web/rodzina/waloryzacja-rent-i-emerytur-w-2025-roku--wzrost-swiadczen-dla-milionow-polakow Juliet is rather conservative in this believe, as her social security benefits will be probably higher than the minimum, especially if she decides to work longer, and claims the benefits at a later age (more about this later). ###### Setting rules for income streams Alright, we have what we need to set up rules triggering different income streams for Juliet, based on her age and the `retirement` event. We're defining a `salary income` stream, which provides funds while Juliet isn't retired. The `social security benefits` stream activates when Juliet retires at 60 (Poland's minimum age for women to claim these benefits) or later. ```{r} #| label: setting expected income household$expected_income <- list( "salary income" = c( glue::glue( "is_not_on('Juliet', 'retirement') ~ {monthly_income * 12}" ) ), "social security benefits" = c(glue::glue( "is_on('Juliet', 'retirement') & age('Juliet') >= 60 ~ ", "{monthly_social_security_benefits * 12}" )) ) household$expected_income ``` ##### Setting expected non-discretionary spending Juliet must identify her essential expenses. Non-discretionary spending covers basic needs such as food, clothing, housing, transport, and medical care. She estimates these costs at **3,500 PLN** monthly for living alone in a big city in Poland [^costs_of_living]. [^costs_of_living]: The costs of leaving for a single in a big city in Poland in 2025 were estimated at **4'000 PLN** per month. This included also discretionary spending like 450 PLN for cinema tickets, eating out, subscriptions. Based on that we assumed that non-discretionary spending is about **3'500 PLN**. See: https://www.bankier.pl/smart/ile-kosztuje-zycie-singla-vs-rodziny-w-2025-budzety-ktore-otwieraja-oczy (in Polish) Let's keep it simple. Non-discretionary spending stays the same, even after retirement. But discretionary spending? That changes. Juliet wants to know how much is optimal for her. ```{r} #| label: setting expected non-discretionary spending household$expected_spending <- list( "total non-discretionary spending" = glue::glue("TRUE ~ {monthly_cost_of_living * 12}") ) household$expected_spending ``` ::: {.callout-important} Non-discretionary spending can vary even within the same category. Take transport, for instance. City bus fares might be essential, yet driving a personal car could be viewed as optional. The distinction often hinges on individual circumstances and assessments. ::: ## Creating Juliet's portfolio Let's set up Juliet's portfolio with a simple template, mostly keeping the defaults. Juliet invests her savings in two assets: a global stock index fund or ETF, and Polish inflation-protected bonds (EDO). She already has some savings in Polish inflation-protected bonds: `r format_currency_custom(1000)` in a taxable account and `r format_currency_custom(500)` in a tax-advantaged account such as IKE. Juliet views her **human capital (discounted future income)** and **liabilities (discounted future non-discretionary spending)** as bond-like—steady and rather uncorrelated to the stock market. This perspective makes sense for many but should be tailored to fit each person's situation[^human_capital]. [^human_capital]: Read more about human capital in [@AreYouAStockOrABond], [@Ibbotson2007LifetimeFinancialAdvice], and [@LifetimeFinancialAdvice2024]. We'll build Juliet's portfolio, incorporating relevant defaults for Poland, such as tax rates. We'll also calculate effective tax rates and the optimal asset allocation for her portfolio. ```{r} #| label: setting portfolio #| output: false portfolio <- create_portfolio_template() portfolio$accounts$taxable <- c(0, 1000) portfolio$accounts$taxadvantaged <- c(0, 500) portfolio$weights$liabilities[1] <- 0.10 portfolio$weights$liabilities[2] <- 1 - portfolio$weights$liabilities[1] portfolio$weights$human_capital[1] <- 0.10 portfolio$weights$human_capital[2] <- 1 - portfolio$weights$human_capital[1] portfolio <- portfolio |> calc_effective_tax_rate( tax_rate_ltcg = 0.19, tax_rate_ordinary_income = 0.19 ) portfolio <- calc_optimal_asset_allocation( household = household, portfolio = portfolio ) ``` We can now display portfolio assumptions and calculation results in the R console. ```{r} #| label: printing portfolio portfolio ``` Output is vast. Let's zero in on the current and optimal allocation, showcasing them together on one plot. ```{r} #| label: plotting optimal portfolio portfolio |> plot_optimal_portfolio() ``` Juliet put all her savings—1'500 PLN—into inflation-protected bonds. But the optimal strategy for her seems to be to move everything into a global stock index fund or ETF, also using tax-advantaged accounts for that. Why? The next sections will reveal more. ::: {.callout-note} The optimal asset allocation here is somewhat similar to the idea of optimal asset allocation based on Merton Share described in this post: [How to Determine Our Optimal Asset Allocation?](https://www.r4good.academy/en/blog/optimal-asset-allocation/index.en.html), but in this case, it also takes into account our lifetime human capital and liabilities. ::: ## Scenario simulations Creating `Household` and `Portfolio` objects sets the stage to simulate various lifetime scenarios for Juliet. ### Simulating basic scenario Let's start our simulations with the most basic scenario: we assume Juliet retires at age 60, and her portfolio performance is based on expected market returns. ```{r} #| label: simulating basic scenario scenario <- simulate_scenario( scenario_id = glue::glue("Juliet retired at {retirement_start_age}"), household = household, portfolio = portfolio ) ``` #### Scenario summary To analyze the simulated data, let's start by creating a table for Juliet with a scenario snapshot for a given year. Our table should capture values relevant to the current (first) year of our scenario simulation (when Juliet is 20 years old). ```{r} #| label: rendering scenario summary scenario |> render_scenario_snapshot(currency = "PLN") ``` Juliet finds actionable insights in the `Expected cashflow` section. Current assumptions suggest her optimal monthly discretionary spending is `r format_currency_custom(round(scenario[1, ]$discretionary_spending / 12))`. Adding non-discretionary expenses, her total spending reaches `r format_currency_custom(round(scenario[1, ]$total_spending / 12))`. She needs to save monthly `r format_currency_custom(round(scenario[1, ]$savings / 12))` and invest it in her optimal portfolio. Juliet's balance sheet summary reveals the present values of three capital types: - **Financial capital**: current value of portfolio assets - **Human capital**: present value of future income streams (salary and pension) - **Liabilities**: present value of future non-discretionary spending Her net worth, calculated as the sum of financial and human capital minus liabilities, shows a positive value. This means her net worth could support discretionary spending. Although her financial assets are modest, her human capital—projected future income—offsets her life-time liabilities. Juliet discovered the essential values from the scenario snapshot table. Let's see how these values evolve over time. #### Plotting expected cash streams Let's dive into Juliet's future income and spending. We'll start with her anticipated non-discretionary spending. This analysis is straightforward, as she has a single, consistent spending stream. It's **3,500 PLN**, adjusted for inflation, and remains steady over time. ```{r} #| label: plotting structure of non-discretionary spending y_limits <- c(NA, 5000) scenario |> plot_future_spending( period = "monthly", type = "non-discretionary", y_limits = y_limits ) ``` Let's consider Juliet's future expected income. ```{r} #| label: plotting structure of future income scenario |> plot_future_income( period = "monthly", y_limits = y_limits ) ``` Her income includes two streams: salary and social security benefits. The salary stops when she retires at age 60. At that point, social security benefits kick in, as 60 is the earliest age women in Poland can claim. Currently, Juliet plans to start these benefits right after retiring. We analyzed income and essential expenses. With this understanding, we can chart Juliet's expected spending—discretionary and non-discretionary. ```{r} #| label: plotting future spending #| classes: preview-image scenario |> plot_future_spending( period = "monthly", discretionary_spending_position = "top", y_limits = y_limits ) ``` We’ve added discretionary spending on top of the non-discretionary spending plot. It starts at `r format_currency_custom(round(scenario[1, ]$discretionary_spending / 12))` per month in the first year and then fluctuates. Why? Several reasons: Discretionary spending hits zero as the chance of being alive drops. Meanwhile, Juliet’s household defaults to certain consumption preferences, showing a mix of consumption impatience and desire for smooth consumption. Each of these preferences shapes how discretionary spending changes over time. We are using some reasonable defaults here, but they can be adjusted to match Juliet's preferences [@LifetimeFinancialAdvice2024, p.17-20]. We will discuss how to adjust these preferences in the later blog posts. Right now, Juliet feels good about her future discretionary spending plans. She's happy with the current setup, allowing her to indulge a bit more sooner rather than later. ::: {.callout-caution} Juliet's savings are invested via both taxable and tax-advantaged accounts. Therefore, her spending should be seen as pre-tax. If she plans to cover her expenses with capital gains from taxable accounts, taxes need to be paid first. This means her true available spending will be lower. ::: #### Plotting expected saving rates Juliet wonders if her saving rate will remain steady, rise, or fall over time. ```{r} #| label: plotting saving rates scenario |> plot_future_saving_rates() ``` Juliet's saving rates hover around 12% but are not flat. They stay relatively stable because her income and necessary spending remain steady. **The key insight for Juliet is that her current saving rate isn't permanent**; it will likely increase over time as Juliet prefers to spend on non-discretionary items a bit more in the nearest future. #### Plotting expected evolution of different capital types Juliet's net worth is shaped by her human and financial capital, along with her liabilities. We can illustrate for Juliet how these elements are expected to change over time. ```{r} #| label: plotting changes in expected capital scenario |> plot_expected_capital() ``` Juliet sees her human capital gradually transform into financial capital, covering both non-discretionary and discretionary expenses. #### Simulating basic scenario with Monte Carlo sampling We've been looking at Juliet’s expected scenario, based on anticipated returns for her portfolio. But Juliet is aware that market returns carry uncertainty. Even with a fixed expected value and volatility, the order of those returns can impact Juliet’s finances negatively. This is known as the risk of sequence of returns. ::: {.callout-tip} Read more about the risk of sequence of returns in this section: [Why is it important to account for the uncertainty of portfolio returns?](https://www.r4good.academy/en/blog/retirement-ruin/index.en.html#why-is-it-important-to-account-for-the-uncertainty-of-portfolio-returns) ::: To address this, we can re-simulate Juliet’s scenario. We'll generate not only the expected returns but also 500 Monte Carlo samples with varied sequences of random returns. ```{r} #| label: simulating basic scenario with multiple Monte Carlo simulations scenario <- simulate_scenario( household = household, portfolio = portfolio, scenario_id = glue::glue( "Juliet retired at {retirement_start_age}" ), monte_carlo_samples = 500, seed = 1234, use_cache = TRUE, auto_parallel = TRUE ) ``` Let's revisit Juliet's future discretionary spending. This time, we'll compare her spending based on expected portfolio returns with spending predictions from various Monte Carlo simulations of potential return sequences. ```{r} #| label: plotting future spending with multiple Monte Carlo simulations scenario |> plot_future_spending("monthly", "discretionary") ``` Juliet notices her discretionary spending shifts with portfolio returns, as shown in the plot. The median spending, marked by a solid dark teal line, drops faster than the expected spending, illustrated by a dashed yellow line. Yet, it remains above 500 PLN most of the time—sufficient in Juliet's view. If returns are unfavorable, Juliet can adapt. She might boost her savings, trim non-essential expenses, consider retiring later, or seek ways to increase her disposable income. ##### One more look at possible future saving rates Juliet noticed that her future savings rate hovers below 15% when her portfolio sees expected returns. But how might these rates shift when averaged across multiple Monte Carlo samples with varying return sequences? ```{r} #| label: plotting saving rates with Monte Carlo simulations aggregated scenario |> plot_future_saving_rates() ``` Triangles on the plot display median saving rates from all Monte Carlo samples. Juliet notices they're rising over time, potentially exceeding 15% due to unfavorable portfolio sequence of returns. If the worst-case scenarios unfolds, Juliet may need to adapt significantly. She might decide to retire later. Fortunately, she still has time to make that decision. For now, she can wait and assess the sequence of returns as they come, then make the best choice based on her current knowledge and future expectations. ### Simulating multiple what-if scenarios Juliet wonders, what if she changes her retirement age? Can she retire a few years early and still maintain her lifestyle? Or, if she enjoys her work, could she continue longer and have more funds for her dreams? Let's create a set of parameters to explore Juliet's options. We'll examine retirement starting at ages 50, 55, 60, 65, and 70. ```{r} #| label: setting parameters for what-if scenarios scenarios_parameters <- tibble::tibble( member = "Juliet", event = "retirement", start_age = seq(50, 70, by = 5), years = Inf, end_age = Inf ) |> dplyr::mutate( scenario_id = paste0(substr(member, 1, 1), "-", start_age) ) |> tidyr::nest(events = -scenario_id) scenarios_parameters |> tidyr::unnest(events) |> print() ``` ```{r} #| label: simulating what-if scenarios #| output: false scenarios <- simulate_scenarios( scenarios_parameters = scenarios_parameters, household = household, portfolio = portfolio, use_cache = TRUE, seeds = 1234 ) ``` After simulating multiple scenarios, let's compare metrics for Juliet's what-if scenarios on one plot. ```{r} #| label: plotting what-if scenarios scenarios |> plot_scenarios("monthly") ``` What this plot shows us? A key takeaway is that Juliet should consider scenarios offering notable metric gains. Take retiring at 50, for example. In the "J-50" scenario (Juliet retiring at 50), her constant discretionary spending[^constant_discretionary_spending] and normalized utility drop to zero. This means **she'd lack enough capital for her expenses**. [^constant_discretionary_spending]: Constant discretionary spending---certainty equivalent constant level of spending that would result in the same lifetime utility as a series of (non-constant) future spending in a given scenario. Now, consider retiring at 55. The "J-55" scenario shows a leap to nearly 400 PLN in constant discretionary spending, **significantly boosting its utility**. What happens if she retires at 60, under the "J-60" scenario? Constant discretionary spending rises to around 800 PLN, but **the utility gain isn't as pronounced**. While later retirement slightly boosts discretionary spending utility, it still raises constant discretionary spending amount, though also at a slower rate. Juliet sees 60 as her target retirement age. Yet, she's curious about shifting the timeline. What if she retires five years earlier or later? #### Simulating multiple what-if scenarios with Monte Carlo sampling Juliet now wants to concentrate on two scenarios she finds most intriguing: retiring at the age of 55 or 65. This time, we plan to generate Monte Carlo samples to conduct a similar analysis to the one we did for the basic scenario (Juliet retiring at 60 years old). This will help us examine how the sequence of risk returns might impact these scenarios differently. ```{r} #| label: simulating selected what-if scenarios with Monte Carlo simulations #| output: false scenarios_parameters <- tibble::tibble( member = "Juliet", event = "retirement", start_age = c(55, 65), years = Inf, end_age = Inf ) |> dplyr::mutate( scenario_id = paste0(substr(member, 1, 1), "-", start_age) ) |> tidyr::nest(events = -scenario_id) scenarios <- simulate_scenarios( scenarios_parameters = scenarios_parameters, household = household, portfolio = portfolio, monte_carlo_samples = 200, use_cache = TRUE, auto_parallel = TRUE, seeds = 1234 ) ``` Let's compare Juliet's what-if scenarios. We'll begin with differences in future discretionary spending. ##### Discretionary spending vs retirement year Juliet wonders how retiring at 55 might affect her discretionary spending. ```{r} #| label: plotting future spending for early retirement y_limits <- c(NA, 1500) scenarios |> dplyr::filter(scenario_id == "J-55") |> plot_future_spending("monthly", "discretionary", y_limits = y_limits) ``` Juliet's early retirement plan requires her to cut discretionary spending to 423 PLN. There's also a **heightened risk of depleting her capital** if returns falter. She's considering now waiting until the age of 65 to retire. Could this boost her future spending potential? ```{r} #| label: plotting future spending for late retirement scenarios |> dplyr::filter(scenario_id == "J-65") |> plot_future_spending("monthly", "discretionary", y_limits = y_limits) ``` If Juliet retires at 65, she can begin spending 1,166 PLN on discretionary items. Even with less favorable returns, she likely has enough capital to cover additional discretionary spending in the hundreds. How might these scenarios affect Juliet's future saving rate? ##### Saving rates vs retirement year Juliet wonders how her saving rates would look if she retires at various ages. ```{r} #| label: plotting future saving rates for early retirement y_limits <- c(NA, 0.25) scenarios |> dplyr::filter(scenario_id == "J-55") |> plot_future_saving_rates(y_limits = y_limits) ``` Juliet realizes she needs to save more—over 20%—if she wants to retire early at 55. ```{r} #| label: plotting future saving rates for late retirement scenarios |> dplyr::filter(scenario_id == "J-65") |> plot_future_saving_rates(y_limits = y_limits) ``` If Juliet retires at 65, she might need to save less—under 10%. However, she may need to boost savings if return rates aren't favorable. ##### Expected asset allocation vs retirement year Juliet's final focus is on tracking how her optimal asset allocation changes across various retirement scenarios. ```{r} #| label: plotting expected asset allocation for early retirement scenarios |> dplyr::filter(scenario_id == "J-55") |> plot_expected_allocation() ``` ```{r} #| label: plotting expected asset allocation for late retirement scenarios |> dplyr::filter(scenario_id == "J-65") |> plot_expected_allocation() ``` In both retirement scenarios, the model advises Juliet to **invest all her financial capital in stocks**. This makes sense because her small financial capital is offset by significant bond-like human capital. As time progresses, the model **recommends moving towards bonds** in both scenarios. However, in the later retirement scenario, the shift to stocks occurs later than in the earlier one. This is because Juliet plans to work longer, maintaining a larger human capital that she will convert into financial capital over an extended period. ## Possible extensions There are several ways in which Juliet can decide to extend the lifecycle model and simulations: 1. We're using two asset types: the risky asset (stocks) and the safe asset (bonds). Our package supports **various assets with specific traits**, though for most, it's likely overkill. Leveraging these two asset classes offers a straightforward, effective approach we endorse, aligning with authors such as [@MissingBillionaires2023] and [@Ibbotson2007LifetimeFinancialAdvice]. 1. We use default market assumptions and Poland-specific tax rates. To **adapt the model for other countries**, update or tailor these elements. You can customize those parameters entirely since the portfolio object functions as an editable data frame, with each asset represented by a single row. 1. We're modeling two income streams for Juliet—her salary and social security benefits—and one non-discretionary spending stream. This setup isn't set in stone. You can tweak it to reflect **various income and spending streams** as Juliet's life events unfold. 1. We've predicted two key moments in Juliet's life: retirement and claiming social security benefits. We could also **consider other significant events**, such as relocating, marriage, having children, or landing a promotion with a raise. Each of these events might have related changes to Juliet's income and spending streams. 1. We've based Juliet's life expectancy on the average for women in Poland. However, this can be **adjusted to match her personal life expectancy**. For instance, if her parents enjoy long lives, she might anticipate a longer lifespan for herself (and tweak the Gompertz parameters). 1. Juliet's household settings use preset values for preferences like consumption impatience, smooth spending, and risk tolerance. You can **adjust these to match Juliet's preferences**—for instance, if she wants to spend more early in life and less later, or vice versa. 1. Juliet plans to claim the minimum social security benefits as early as possible during retirement. It's worth evaluating if delaying her claim could offer more advantages. The next versions of the package will **include custom functions to dynamically calculate income streams based on events** like age when you begin claiming social security benefits. ::: {.callout-tip} ## When to claim social security pension? We assumed Juliet will only claim the minimum social security benefits at retirement. That may be too pessimistic. Even if the average pension replacement rate for young people like Juliet in Poland might be around 40% [@oecd2023pensions, p.53-54], Juliet could still receive roughly 2,000 PLN per month at age 60 in today's terms. That's a bit more than the current minimum social security benefits (`r format_currency(monthly_social_security_benefits)`).   Moreover, Juliet's social security pension will grow if she waits before claiming it. Delaying each year boosts her pension by 8-10% [^pension_delay]. Waiting for 10 years, until age 70, could increase Juliet's pension to 4,000 PLN or more. [^pension_delay]: See article (in Polish): https://businessinsider.com.pl/praca/emerytury/emerytura-jak-uzyskac-wyzsze-swiadczenie-ike-ppk-odroczenie-emerytury-prezes-zus/cx88knm. The similar situation is in US, where Social Security payments increase 8 percent for every year after full retirement age that a retiree waits to claim benefits. A retiree who des not take early Social Security benefits may enjoy a benefit up to 30 percent grater than one who receives benefits at the earliest possible age. [@cfpboard2015competency, p.437] ```{r} #| label: pension_calculations #| echo: false #| eval: false 0.40 * 6482 0.40 * 4995 (0.40 * 4995) * 1.08^10 2000 * 1.08^10 2000 * 1.10^10 ``` Should Juliet delay claiming Social Security? That is a topic for another post. But it's worth considering in her financial model. **Social Security works like an inflation-indexed annuity** from the recipient’s perspective [@Ibbotson2007LifetimeFinancialAdvice, p.vii]. This makes it **crucial insurance against outliving ones savings**. ::: ## Conclusion Juliet thrives solo in a single-person household in a bustling Polish city. She navigates life independently, whether or not Romeo is by her side, or if they haven’t crossed paths, or perhaps they did, but he wasn’t quite right for her. Our simulations suggest this **single-person household scenario is realistic for Juliet**. Juliet bases her decisions on **current assumptions** about the future market and a median salary that aligns with inflation. The **future is uncertain**, which means these assumptions might shift. However, **decisions must be made today, rooted in what seems most reasonable right now**. **When the future looks bleak, Juliet will adapt**. She might ramp up her savings, cut unnecessary costs, think about retiring later, or find ways to boost her income—like taking on part-time work or seizing business opportunities. But if the future shines bright, she could decide to enjoy more discretionary spending, retire earlier, or even do both. **You can see that with the household lifecycle framework you can quite quickly reach an optimal (or near-optimal) recommendation tailored to your own specific situation at a given moment.** In future posts, we'll explore scenarios where Juliet and Romeo choose to spend their life together. Our simulation will include diverse income sources, multiple necessary expenses, and varied life expectancy assumptions. Eventually, we'll even factor in children. ::: {.callout-tip} Enjoyed this post? **Share it** with others who might find it interesting. **Subscribe to our newsletter** to stay updated. Thanks for reading! :::

Meet Juliet

Juliet’s assumptions and expectations

Setting up the technical essentials for the report

Loading the package

Setting the date of the report

Creating Juliet’s household

Defining the household member

Setting Gompertz parameters for Juliet

Defining Juliet’s household

Defining income and spending expectations

Setting the retirement event

Setting expected disposable income streams

Salary income

Pension income

Setting rules for income streams

Setting expected non-discretionary spending

Creating Juliet’s portfolio

Scenario simulations

Simulating basic scenario

Scenario summary

Plotting expected cash streams

Plotting expected saving rates

Plotting expected evolution of different capital types

Simulating basic scenario with Monte Carlo sampling

One more look at possible future saving rates

Simulating multiple what-if scenarios

Simulating multiple what-if scenarios with Monte Carlo sampling

Discretionary spending vs retirement year

Saving rates vs retirement year

Expected asset allocation vs retirement year

Possible extensions

Conclusion

References

Footnotes

Citation

Setting the `retirement` event